
分析 根据题意,设P(4,t).
(I)设两切点为C,D,则OC⊥PC,OD⊥PD,由题意可知|PO|2=|OC|2+|PC|2,即42+t2=4+12,解得t=0,所以点P坐标为(4,0),由此能够求出两切线所夹劣弧长;
(II)设M(x1,y1),N(x2,y2),Q(1,0),依题意,直线PA经过点A(-2,0),P(4,t),可以设AP:y=$\frac{t}{6}$(x+2),和圆x2+y2=4联立,代入消元得到,(t2+36)x2+4t2x+4t2-144=0,因为直线AP经过点A(-2,0),M(x1,y1),所以-2,x1是方程的两个根,然后由根与系数的关系进行求解.
解答 解:根据题意,设P(4,t).
(1)设两切点为C,D,则OC⊥PC,OD⊥PD,
由题意可知|PO|2=|OC|2+|PC|2,即42+t2=4+12(2分)
解得t=0,所以点P坐标为(4,0).(3分)
在Rt△POC中,易得∠POC=60°.(4分)
所以两切线所夹劣弧长为$\frac{2π}{3}×2=\frac{4π}{3}$.(5分)
(II)设M(x1,y1),N(x2,y2),Q(1,0),
依题意,直线PA经过点A(-2,0),P(4,t),
可以设AP:y=$\frac{t}{6}$(x+2),(6分)
和圆x2+y2=4联立,代入消元得到,(t2+36)x2+4t2x+4t2-144=0,(7分)
因为直线AP经过点A(-2,0),M(x1,y1),所以-2,x1是方程的两个根,
所以有-2x1=$\frac{4{t}^{2}-144}{{t}^{2}+36}$,x1=$\frac{72-2{t}^{2}}{{t}^{2}+36}$,(8分)
代入直线方程y=$\frac{t}{6}$(x+2),得y1=$\frac{24t}{{t}^{2}+36}$.(9分)
同理,设BP:y=$\frac{t}{2}$(x-2),和圆x2+y2=4联立,代入消元得到(4+t2)x2-4t2x+4t2-16=0,
因为直线BP经过点B(2,0),N(x2,y2),所以2,x2是方程的两个根,x2=$\frac{2{t}^{2}-8}{{t}^{2}+4}$,
代入y=$\frac{t}{2}$(x-2),得到y2=$\frac{-8t}{{t}^{2}+4}$.(11分)
若x1=1,则t2=12,此时x2=$\frac{2{t}^{2}-8}{{t}^{2}+4}$=1
显然M,Q,N三点在直线x=1上,即直线MN经过定点Q(1,0)(12分)
若x1≠1,则t2≠12,x2≠1,
所以有kMQ=$\frac{8t}{12-{t}^{2}}$,kNQ=$\frac{8t}{12-{t}^{2}}$,(13分)
所以kMQ=kNQ,所以M,N,Q三点共线,
即直线MN经过定点Q(1,0).
综上所述,直线MN经过定点Q(1,0).(14分)
点评 本题考查直线和圆的位置关系,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (3,+∞) | B. | (0,$\frac{1}{4}$] | C. | (1,3) | D. | [$\frac{1}{4}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
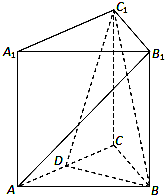 三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.
三棱ABC-A1B1C1,A1A⊥底面ABC,且△ABC为正三角形,且,D为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
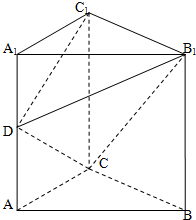 如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.
如图在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=BC=2AC=2,D为AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com