
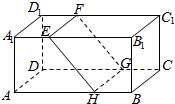
 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.分析 (1)利用平行公理证出平行四边形,根据数据计算得出邻边相等,根据线面垂直得出邻边垂直;
(2)两部分都是侧放的直棱柱且高相等,故体积比为底面积的比.
解答 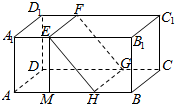 证明:(1)∵A1E=D1F,A1E∥D1F,
证明:(1)∵A1E=D1F,A1E∥D1F,
∴四边形A1EFD1是平行四边形,∴EF∥A1D1,EF=A1D1,
同理,HG∥AD,HG=AD,∴EF∥HG,EF=HG.
∴四边形EFGH是平行四边形,
过点E作EM⊥AB,垂足为M,则EM=AA1=8,AM=A1E=4,
∴MH=AH-AM=6,EH=$\sqrt{E{M}^{2}+M{H}^{2}}$=10,∴EF=EH,
∴四边形EFGH是菱形.
∵A1D1⊥平面ABB1A1,EF∥A1D1,
∴EF⊥平面ABB1A1,∵EH?平面ABB1A1,
∴EF⊥EH,∴四边形EFGH是正方形.
(2)EB1=A1B1-A1E=12,HB=AB-AH=6,
S${\;}_{梯形AHE{A}_{1}}$=$\frac{1}{2}$(A1E+AH)•AA1=7AA1,S${\;}_{梯形HB{B}_{1}E}$=$\frac{1}{2}$(HB+B1E)•AA1=9AA1,
∴$\frac{{V}_{1}}{{V}_{2}}$=$\frac{7}{9}$.
点评 本题考查了线面平行的性质和几何体的体积计算,属于基础题.


 优百分课时互动系列答案
优百分课时互动系列答案科目:高中数学 来源: 题型:解答题
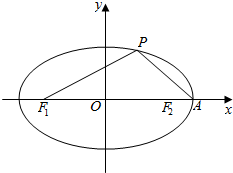 如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$
如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {(-1,1)} | B. | {(0,1)} | C. | [-1,0] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
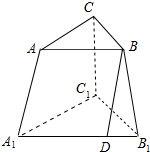 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )| A. | 平面 | B. | 直线 | ||
| C. | 线段,但只含1个端点 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com