
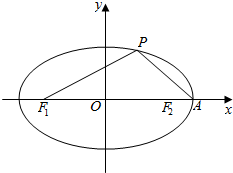
 如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$
如图,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,A为椭圆的右顶点,点P在椭圆上且∠PF1F2=arccos$\frac{7}{8}$分析 (1)根据椭圆的性质,可得|PF1|=x,则|PF2|=10-x,|F1F2|=2$\sqrt{25-9}$=8,结合已知可余弦定理构造方程,解得x值;
(2)由出sin∠PF1F2,进而计算△PF1F2的面积,可得P到x轴的距离d,结合△PF1A的底边|F1A|=a+c=9,可得三角形面积.
解答 解:(1)∵椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1的左、右两个焦点分别为F1、F2,P为椭圆上一点,
|PF1|=x,则|PF2|=10-x,|F1F2|=2$\sqrt{25-9}$=8,
∵∠PF1F2=arccos$\frac{7}{8}$,
故cos∠PF1F2=$\frac{7}{8}$=$\frac{{x}^{2}+{8}^{2}-{(10-x)}^{2}}{2×8x}$,
解得:x=6,
(2)由∠PF1F2=arccos$\frac{7}{8}$,可得:sin∠PF1F2=$\sqrt{1-(\frac{7}{8})^{2}}$=$\frac{\sqrt{15}}{8}$,
故△PF1F2的面积S=$\frac{1}{2}$(5+$\frac{\sqrt{385}}{5}$)•(5-$\frac{\sqrt{385}}{5}$)•$\frac{\sqrt{15}}{8}$=$\frac{7\sqrt{15}}{20}$,
故P到x轴的距离d=$\frac{2S}{8}$=$\frac{7\sqrt{15}}{80}$,
由|F1A|=a+c=9,可得△PF1A的面积为:$\frac{1}{2}×9$×$\frac{7\sqrt{15}}{80}$=$\frac{63\sqrt{15}}{160}$
点评 本题考查的知识点是椭圆的简单性质,余弦定理,三角形面积公式,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{\frac{3}{2}}}$ | C. | y=x-2 | D. | $y={x^{-\frac{1}{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,4} | B. | {2,3} | C. | {4} | D. | {2,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
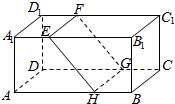 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com