
分析 (Ⅰ)利用汽车的速度为30千米/小时,则刹车距离为6.5米.求出函数的解析式,然后当汽车时速为60千米/小时,代入求解可得其刹车距离.
(Ⅱ)利用函数的解析式,代入刹车距离大于49.5米,然后该车在道路上行驶速度即可.
解答 解:(Ⅰ)$S=av+\frac{1}{180}{v^2}$,若该种汽车的速度为30千米/小时,则刹车距离为6.5米.
可得6.5=30a+$\frac{1}{180}×{30}^{2}$,
解得a=$\frac{1}{20}$,
$S=\frac{1}{20}v+\frac{1}{180}{v}^{2}$,
汽车时速为60千米/小时,其刹车距离为:$S=\frac{1}{20}×60+\frac{1}{180}×{60}^{2}$=23米.
(Ⅱ)交警测得该种车的刹车距离大于49.5米,由$S=\frac{1}{20}v+\frac{1}{180}{v}^{2}$,
可得$\frac{1}{20}v+\frac{1}{180}{v}^{2}>49.5$,v2+9v-8910>0,
解得v>$\frac{-9+\sqrt{81+35640}}{2}$=$\frac{-9+189}{2}$=90.
该车的速度超过90千米/小时,超速行驶.
点评 本题考查函数的解析式的应用,不等式的解法,考查分析问题解决问题的能力.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $y={x^{\frac{2}{3}}}$ | B. | $y={x^{\frac{3}{2}}}$ | C. | y=x-2 | D. | $y={x^{-\frac{1}{2}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{19}}}{2}$ | D. | $\frac{{2\sqrt{19}}}{19}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
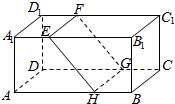 如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.
如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4,点H,G分别在AB,CD上,AH=DG=10.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com