
分析 (1)可求出f(x)的对称轴为x=a,而要使y=f(x)在[-5,5]上单调递减,则需满足a≥5,这便得到了a的取值范围;
(2)可讨论对称轴x=a和区间[-5,5]的关系:分a≤-5,-5<a<5,和a≥5三种情况,然后根据f(x)在[-5,5]上的单调性及取得顶点情况求出每种情况的f(x)的最小值,从而便可得出g(a)的解析式.
解答 解:(1)函数f(x)的对称轴为x=a;
∵f(x)在[-5,5]上是单调递减函数;
∴a≥5;
∴实数a的取值范围为[5,+∞);
(2)①当a≤-5时,f(x)在[-5,5]上单调递增;
∴f(x)min=f(-5)=27+10a;
②当-5<a<5时,$f(x)_{min}=f(a)=-{a}^{2}+2$;
③当a≥5时,f(x)在[-5,5]上单调递减;
∴f(x)min=f(5)=27-10a;
∴$g(a)=\left\{\begin{array}{l}{27+10a}&{a≤-5}\\{-{a}^{2}+2}&{-5<a<5}\\{27-10a}&{a≥5}\end{array}\right.$.
点评 考查二次函数的对称轴,二次函数的单调性,以及根据二次函数的单调性及取得顶点情况求其在闭区间上的最小值的方法.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 4x-13y-20=0或4x+13y-20=0 | B. | 2x-3y-10=0或2x+3y-10=0 | ||
| C. | 6x+5y-30=0或6x-5y-30=0 | D. | 4x+9y-20=0或2x+3y-10=0. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
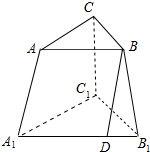 在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )
在三棱台A1B1C1-ABC中,点D在A1B1上,且AA1∥BD,点M是△A1B1C1内(含边界)的一个动点,且有平面BDM∥平面A1C,则动点M的轨迹是( )| A. | 平面 | B. | 直线 | ||
| C. | 线段,但只含1个端点 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11-5ln2}{2}$ | B. | 2 | C. | 8-5ln2 | D. | 7-5ln2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [-1,1] | C. | [-$\sqrt{2}$,$\sqrt{2}$] | D. | [-$\frac{1}{2}$,$\frac{1}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com