
分析 根据两向量平行的坐标表示,列出方程求出x的值,再求$\overrightarrow{a}$+$\overrightarrow{b}$的模长|$\overrightarrow{a}$+$\overrightarrow{b}$|.
解答 解:∵向量$\overrightarrow{a}$=(4,-2),$\overrightarrow{b}$=(x,1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴-2x-4×1=0,解得x=-2;
∴$\overrightarrow{b}$=(-2,1),
∴$\overrightarrow{a}$+$\overrightarrow{b}$=(2,-1),
∴|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{{2}^{2}{+(-1)}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了平面向量的坐标运算问题,也考查了向量平行与模长的计算问题,是基础题目.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | ①和② | B. | ①和③ | C. | ②和④ | D. | ①和④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
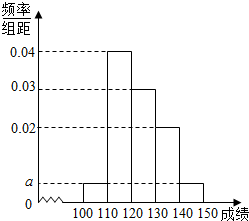 贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].
贵阳市某中学高三第一次摸底考试中100名学生数学成绩的频率分布直方图如图所示,其中成绩分组区间是[100,110),[110,120),[120,130),[130,140),[140,150].| 分数段 | [100,110) | [110,120) | [120,130) | [130,140) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
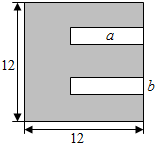 如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )
如图所示:一张正方形状的黑色硬质板,剪去两个一样的小矩形得到一个“E”形的图形,设小矩形的长、宽分别为a,b(2≤a≤10),剪去部分的面积为8,则$\frac{1}{b+1}$+$\frac{9}{a+9}$的最大值为( )| A. | 1 | B. | $\frac{11}{10}$ | C. | $\frac{6}{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com