
【题目】2020年是我国垃圾分类逐步凸显效果关键的一年.在国家高度重视,重拳出击的前提下,高强度、高频率的宣传教育能有效缩短我国生活垃圾分类走入世界前列所需的时间,打好垃圾分类这场“持久战”,“全民战”.某市做了一项调查,在一所城市中学和一所县城中学随机各抽取15名学生,对垃圾分类知识进行问答,满分为100分,他们所得成绩如下:
城市中学学生成绩分别为:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
县城中学学生成绩分别为:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根据上述两组数据在图中完成两所中学学生成绩的茎叶图,并通过茎叶图比较两所中学学生成绩的平均分及分散程度;(不要求计算出具体值,给出结论即可)
(2)从城市中学成绩在80分以上的学生中抽取4名,记这4名学生的成绩在90分以上的人数为X,求X的分布列与数学期望.
【答案】(1)茎叶图见解析,城市中学的平均分高于县城中学平均分,城市中学学生成绩比较集中,县城中学学生成绩比较分散;(2)分布列见解析,![]() .
.
【解析】
(1)县城中学学生成绩60段有5人,70分段有7人,80分段2人,90分段1人,共四个分数段;城市中学学生成绩60段有0人,70分段有5人,80分段7人,90分段3人,共三个分数段;城市中学学生成绩平均分高一些,也相对集中.
(2)城市中学成绩 80分以上的学生共有10名,93分以上的学生共有3名, 从城市中学成绩在80分以上的学生中抽取4名,因此![]() ,1,2,3,由古典概型计算各个概率,列出分布列,后求期望即可.
,1,2,3,由古典概型计算各个概率,列出分布列,后求期望即可.
解:(1)茎叶图如图所示.
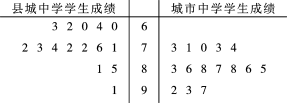
城市中学的平均分高于县城中学平均分,
城市中学学生成绩比较集中,县城中学学生成绩比较分散.
(2)80分以上的学生共有10名,93分以上的学生共有3名,
由题可知![]() ,1,2,3,
,1,2,3,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
X的分布列为
|
|
|
|
|
|
|
|
|
|
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系中,曲线C的参数方程为![]() 为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为
为参数),以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线D的极坐标方程为![]() .
.
(1)写出曲线C的极坐标方程以及曲线D的直角坐标方程;
(2)若过点![]() (极坐标)且倾斜角为
(极坐标)且倾斜角为![]() 的直线l与曲线C交于M,N两点,弦MN的中点为P,求
的直线l与曲线C交于M,N两点,弦MN的中点为P,求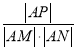 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
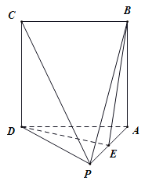
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,正方形
,正方形![]() 边长为2,
边长为2,![]() 是
是![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的长度;
的长度;
(3)若![]() ,线段
,线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 平面
平面![]() ,若存在求
,若存在求![]() 的长度,若不存在则说明.
的长度,若不存在则说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,P,Q,M,N,H,R是各条棱的中点.
中,P,Q,M,N,H,R是各条棱的中点.
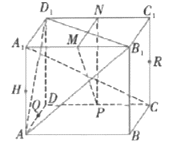
①直线![]() 平面
平面![]() ;②
;②![]() ;③P,Q,H,R四点共面;④
;③P,Q,H,R四点共面;④![]() 平面
平面![]() .其中正确的个数为( )
.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年是我国垃圾分类逐步凸显效果关键的一年.在国家高度重视,重拳出击的前提下,高强度、高频率的宣传教育能有效缩短我国生活垃圾分类走入世界前列所需的时间,打好垃圾分类这场“持久战”,“全民战”.某市做了一项调查,在一所城市中学和一所县城中学随机各抽取15名学生,对垃圾分类知识进行问答,满分为100分,他们所得成绩如下:
城市中学学生成绩分别为:73 71 83 86 92 70 88 93 73 97 87 88 74 86 85
县城中学学生成绩分别为:60 64 71 91 60 76 72 85 81 72 62 74 73 63 72

(1)根据上述两组数据在图中完成两所中学学生成绩的茎叶图,并通过茎叶图比较两所中学学生成绩的平均分及分散程度;(不要求计算出具体值,给出结论即可)
(2)记这30名学生成绩80分以上为良好,80分以下为一般,完善表格,并判断是否有99%的把握认为该城市中学和县城中学的学生在了解垃圾分类知识上有差异?(结果保留三位小数)
学生成绩 | 良好 | 一般 | 合计 |
城市中学学生 | |||
县城中学学生 | |||
合计 |
附: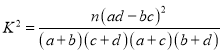 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
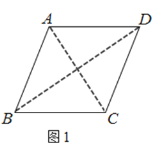
【题目】已知四边形![]() 是边长为5的菱形,对角线
是边长为5的菱形,对角线![]() (如图1),现以
(如图1),现以![]() 为折痕将菱形折起,使点
为折痕将菱形折起,使点![]() 达到点
达到点![]() 的位置,棱
的位置,棱![]() ,
,![]() 的中点分为
的中点分为![]() ,
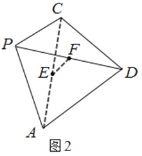
,![]() ,且四面体
,且四面体![]() 的外接球球心落在四面体内部(如图2),则线段
的外接球球心落在四面体内部(如图2),则线段![]() 长度的取值范围为________.
长度的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() 、
、![]() ,离心率为
,离心率为![]() ,点P是椭圆C上的一个动点,且
,点P是椭圆C上的一个动点,且![]() 面积的最大值为
面积的最大值为![]() .
.
(1)求椭圆C的方程;
(2)椭圆C与x轴交于A、B两点,直线![]() 和
和![]() 与直线l:
与直线l:![]() 分别交于点M,N,试探究以
分别交于点M,N,试探究以![]() 为直径的圆是否恒过定点,若是,求出所有定点的坐标:若否,请说明理由.
为直径的圆是否恒过定点,若是,求出所有定点的坐标:若否,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com