
| A. | $\frac{2\sqrt{2}}{9}$ | B. | $\frac{2\sqrt{3}}{9}$ | C. | $\frac{2\sqrt{2}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 作出图形,找到三个棱锥的公共部分,利用相似三角形得出公共部分棱锥的高,代入体积公式计算.
解答 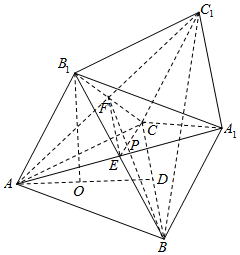 解:设菱形ABB1A1的中心为E,菱形BCC1B1的中心为F,连结CE,AF交点为P,则四面体A1-ABC,B1-ABC,C1-ABC公共部分为三棱锥P-ABC.
解:设菱形ABB1A1的中心为E,菱形BCC1B1的中心为F,连结CE,AF交点为P,则四面体A1-ABC,B1-ABC,C1-ABC公共部分为三棱锥P-ABC.
取底面ABC的中心O,连结B1O,则B1O⊥平面ABC.
延长BO交AC于D,则D为AC的中点,
∵AB=BC=AC=2,O是正三角形ABC的中心,
∴BD=$\sqrt{A{B}^{2}-A{D}^{2}}$=$\sqrt{3}$,BO=$\frac{2}{3}$BD=$\frac{2\sqrt{3}}{3}$.
∴B1O=$\sqrt{B{{B}_{1}}^{2}-B{O}^{2}}$=$\frac{2\sqrt{6}}{3}$.
∵EF$\stackrel{∥}{=}$$\frac{1}{2}$AC,∴△PEF∽△PCA,
∴$\frac{PE}{PC}=\frac{EF}{AC}=\frac{1}{2}$,
又∵E是B1A的中点,∴P到底面ABC的距离h=$\frac{1}{2}{B}_{1}O$×$\frac{2}{3}$=$\frac{2\sqrt{6}}{9}$.
∴VP-ABC=$\frac{1}{3}{S}_{△ABC}•h$=$\frac{1}{3}×\frac{\sqrt{3}}{4}×{2}^{2}×\frac{2\sqrt{6}}{9}$=$\frac{2\sqrt{2}}{9}$.
故选A.
点评 本题考查了棱锥的结构特征,棱锥的体积计算,求出公共部分的高是解题关键.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )
如图是高二数学选修1-2第二章“推理与证明”的知识结构图,已知反证法是一种间接证明方法,如果要在图中加入反证法,则应把它放在( )| A. | “合情推理”的下位 | B. | “演绎推理”的下位 | ||
| C. | “直接证明”的下位 | D. | “间接证明”的下位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
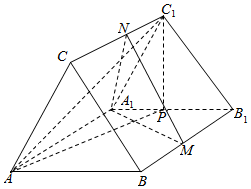 如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.
如图,直三棱柱ABC-A1B1C1中,△ABC是正三角形,AB=AA1,M是BB1的中点,P是A1B1的中点,N是线段CC1上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a=1,b=1 | B. | a=3,b=1 | C. | a=1,b=0 | D. | a=3,b=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 数列4,7,3,4的首项是4 | |
| B. | 数列{an}中,若a1=3,则从第2项起,各项均不等于3 | |
| C. | 数列-1,0,1,2与数列0,1,2,-1不相同 | |
| D. | 数列中的项不能是三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com