
分析 (I)由$\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{5}}}{5}\\ c=1\end{array}\right.$,及a2=b2+c2,解出即可得出;
(II)①当k不存在时,直线l:x=1,与椭圆方程联立解出即可得出.
②当k存在时,设直线l:y=k(x-1),弦端点为M(x1,y1),N(x2,y2),与椭圆方程联立化为:(4+5k2)x2-10k2x+5k2-20=0,利用根与系数的关系、向量数量积运算性质即可得出.
解答 解:(I)由$\left\{\begin{array}{l}\frac{c}{a}=\frac{{\sqrt{5}}}{5}\\ c=1\end{array}\right.$,及a2=b2+c2,解得$\left\{\begin{array}{l}a=\sqrt{5}\\ b=2\\ c=1\end{array}\right.$,
∴椭圆的标准方程为$\frac{x^2}{5}+\frac{y^2}{4}=1$.
(II)①当k不存在时,直线l:x=1,
由$\left\{\begin{array}{l}x=1\\ \frac{x^2}{5}+\frac{y^2}{4}=1\end{array}\right.$,得交点$M(1,\frac{{4\sqrt{5}}}{5}),N(1,-\frac{{4\sqrt{5}}}{5})$,
∴$\overrightarrow{OM}•\overrightarrow{ON}=-\frac{11}{5}$,与题不符,舍去.
②当k存在时,设直线l:y=k(x-1),弦端点为M(x1,y1),N(x2,y2),
由$\left\{\begin{array}{l}y=k(x-1)\\ \frac{x^2}{5}+\frac{y^2}{4}=1\end{array}\right.$,得(4+5k2)x2-10k2x+5k2-20=0,
∴$\left\{\begin{array}{l}{x_1}+{x_2}=\frac{{10{k^2}}}{{5{k^2}+4}}\\{x_1}{x_2}=\frac{{5{k^2}-20}}{{5{k^2}+4}}\\ \\△>0⇒k∈R\end{array}\right.$,
∴$\overrightarrow{OM}•\overrightarrow{ON}=-\frac{31}{9}$,得${x_1}{x_2}+{y_1}{y_2}=-\frac{31}{9}$,
即$(1+{k^2}){x_1}{x_2}-{k^2}({x_1}+{x_2})+{k^2}+\frac{31}{9}=0$,
∴k=±1即直线l方程为l:y=±(x-1),
综上①②可知,直线l方程为l:y=±(x-1).
点评 本题考查了椭圆的标准方程及其性质、一元二次方程的根与系数的关系、向量的数量积运算性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
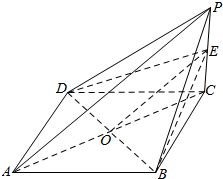 如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.
如图所示,在四棱锥P-ABCD中,四边形ABCD是边长为2的正方形,平面ABCD⊥平面PCD,∠PCD=90°,PC=1.5,E是侧棱PC上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
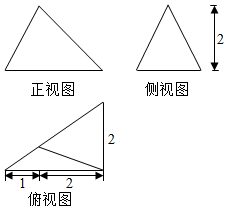
| A. | $\frac{4}{3}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com