
【题目】已知一条动直线3(m+1)x+(m-1)y-6m-2=0,
(1)求证:直线恒过定点,并求出定点P的坐标;
(2)若直线与x、y轴的正半轴分别交于A,B两点,O为坐标原点,是否存在直线满足下列条件:①△AOB的周长为12;②△AOB的面积为6,若存在,求出方程;若不存在,请说明理由.
(3)若直线与x、y轴的正半轴分别交于A,B两点,当![]() 取最小值时,求直线的方程.
取最小值时,求直线的方程.
【答案】(1)证明见解析;![]() (2)存在;直线方程为3x+4y-12=0(3)3x+3y-10=0
(2)存在;直线方程为3x+4y-12=0(3)3x+3y-10=0
【解析】
(1)将题目所给直线方程重新整理,由此证得直线恒过定点,并求得定点坐标.
(2)设出直线方程截距式,根据题目所给条件,求出直线方程.
(3)设出直线的倾斜角,求得![]() 的表达式并结合三角函数的知识求得最小值,以及此时的直线方程.
的表达式并结合三角函数的知识求得最小值,以及此时的直线方程.
(1)依题意直线方程为![]() ,
,
即![]() ,
,
即![]() ,
,
所以由![]() ,解得
,解得![]() ,故直线过定点
,故直线过定点![]() .
.
(2)依题意设直线方程为![]() ,将
,将![]() 代入得
代入得![]() ①.
①.
则![]() ,则
,则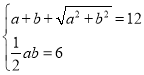 ,解得
,解得![]() 或
或![]() .
.
其中![]() 不满足①,
不满足①,![]() 满足①.
满足①.
所以存在直线![]() ,即
,即![]() 满足条件.
满足条件.
(3)由(1)知直线过定点![]() ,而若直线与x、y轴的正半轴分别交于A,B两点,所以直线的倾斜角
,而若直线与x、y轴的正半轴分别交于A,B两点,所以直线的倾斜角![]() ,
,
所以![]() ,
,
所以![]() ②,
②,
令![]() ,
,
由于![]() ,所以
,所以![]() ,所以
,所以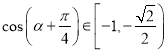 ,
,
所以![]() .
.
则②可化为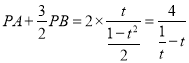 ,由于
,由于![]() 在
在![]() 上为减函数,所以
上为减函数,所以![]() 在
在![]() 上为增函数,故当
上为增函数,故当![]() ,即
,即![]() 时,
时,![]() 取得最小值为
取得最小值为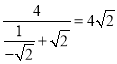 .此时直线方程为
.此时直线方程为![]() ,即
,即![]() ,
,
也即![]() .
.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x![]() )+a的最大值为2.
)+a的最大值为2.
(1)求实数a的值;
(2)在给定的直角坐标系上作出函数f(x)在[0,π]上的图象:
(3)求函数f(x)在[![]() ,
,![]() ]上的零点,
]上的零点,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为8.
的周长为8.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,侧面
的菱形,侧面![]() 底面
底面![]() ,
,![]() ,
, ![]() ,
, ![]() 是
是![]() 中点,点
中点,点![]() 在侧棱
在侧棱![]() 上.
上.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)若![]() 是
是![]() 中点,求二面角
中点,求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)是否存在![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明家的晚报在下午![]() 任何一个时间随机地被送到,他们一家人在下午
任何一个时间随机地被送到,他们一家人在下午![]() 任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,
任何一个时间随机地开始晚餐.为了计算晚报在晚餐开始之前被送到的概率,某小组借助随机数表的模拟方法来计算概率,他们的具体做法是将每个1分钟的时间段看作个体进行编号,![]() 编号为01,
编号为01,![]() 编号为02,依此类推,
编号为02,依此类推,![]() 编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数6548中的65不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为( )
编号为90.在随机数表中每次选取一个四位数,前两位表示晚报时间,后两位表示晚餐时间,如果读取的四位数表示的晚报晚餐时间有一个不符合实际意义,视为这次读取的无效数据(例如下表中的第一个四位数6548中的65不符合晚报时间).按照从左向右,读完第一行,再从左向右读第二行的顺序,读完下表,用频率估计晚报在晚餐开始之前被送到的概率为( )
6548 1176 7417 4685 0950 5804 7769 7473 0395 7186 |
8012 4356 3517 7270 8015 4531 8223 7421 1157 8263 |
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com