
分析 (1)当$a=\frac{1}{2}$时,?n∈N+,(-1)n•2<2+$\frac{(-1)^{n+1}}{n}$,当n为偶数时,2<2-$\frac{1}{n}$不成立.
当$|{x-\frac{5}{2}}|<a({a>0})$时,⇒2<x<3⇒-1<x2-5<4⇒不等式|x2-5|<4成立.
(2)命题p为真命题时:当n为偶数时,2a+1<2-$\frac{1}{n}$恒成立⇒2a+1<(2-$\frac{1}{n}$)min,⇒a<$\frac{1}{4}$,
当n为奇数时,-(2a+1)<2+$\frac{1}{n}$恒成立⇒-(2a+1)<(2+$\frac{1}{n}$)min,⇒-(2a+1)≤2⇒a≥-$\frac{3}{2}$.
命题q为真命题时:$|{x-\frac{5}{2}}|<a({a>0})$的解集为($\frac{5}{2}-a,\frac{5}{2}+a$),不等式|x2-5|<4的解集为:(-3,-1)∪(1,3)
由($\frac{5}{2}-a,\frac{5}{2}+a$)⊆3,-1)∪(1,3)⇒0<a≤$\frac{1}{2}$,
如果p∧q为假命题,p∨q为真命题,则p、q为一真一假,列式计算;
解答 解:(1)当$a=\frac{1}{2}$时,命题$p:?n∈{N^*},{({-1})^n}•({2a+1})<2+\frac{{{{({-1})}^{n+1}}}}{n}$??n∈N+,(-1)n•2<2+$\frac{(-1)^{n+1}}{n}$,当n为偶数时,2<2-$\frac{1}{n}$不成立,故命题p为假命题.
当$|{x-\frac{5}{2}}|<a({a>0})$时,⇒2<x<3⇒-1<x2-5<4⇒不等式|x2-5|<4成立,故命题q为真命题.
(2)命题p为真命题时:当n为偶数时,2a+1<2-$\frac{1}{n}$恒成立⇒2a+1<(2-$\frac{1}{n}$)min,⇒a<$\frac{1}{4}$,
当n为奇数时,-(2a+1)<2+$\frac{1}{n}$恒成立⇒-(2a+1)<(2+$\frac{1}{n}$)min,⇒-(2a+1)≤2⇒a≥-$\frac{3}{2}$.
故命题p为真命题时:-$\frac{3}{2}$≤a<$\frac{1}{4}$.
命题q为真命题时:$|{x-\frac{5}{2}}|<a({a>0})$的解集为($\frac{5}{2}-a,\frac{5}{2}+a$),不等式|x2-5|<4的解集为:(-3,-1)∪(1,3)
由($\frac{5}{2}-a,\frac{5}{2}+a$)⊆3,-1)∪(1,3)⇒0<a≤$\frac{1}{2}$,
故命题q为真命题时:0<a≤$\frac{1}{2}$,
如果p∧q为假命题,p∨q为真命题,则p、q为一真一假;
即$\left\{\begin{array}{l}{-\frac{3}{2}≤a<\frac{1}{4}}\\{a≤0或a>1}\end{array}\right.得-\frac{3}{2}≤a≤0$或$\left\{\begin{array}{l}{a<-\frac{3}{2}或a≥\frac{1}{4}}\\{0<a≤\frac{1}{2}}\end{array}\right.得\frac{1}{4}≤a≤\frac{1}{2}$
综上实数a的取值范围:[-$\frac{3}{2},0$]∪[$\frac{1}{4}$,$\frac{1}{2}$].
点评 本题考查了命题真假的应用,涉及到了不等式、恒成立的运算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3π | B. | 4π | C. | 5π | D. | 6π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
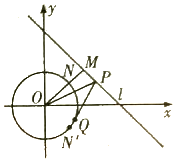 已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.
已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②④ | C. | ①③ | D. | ② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com