
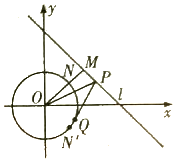
 已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.
已知圆O:x2+y2=2,直线l过点$M(\frac{3}{2},\frac{3}{2})$,且OM⊥l,P(x0,y0)是直线l上的动点,线段OM与圆O的交点为点N,N'是N关于x轴的对称点.分析 (1)OM⊥l,直线l上的斜率为-1,即可求直线l的方程;
(2)对每个给定的点P,当PQ为圆O的切线时,∠OPQ最大,此时OQ⊥PQ,即可求x0的取值范围;
(3)已知A,B是圆O上不同的两点,且∠ANN'=∠BNN',求出A,B的坐标,即可证明直线AB的斜率为定值.
解答 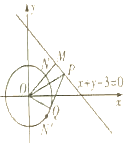 解:(1)∵OM⊥l,∴直线l上的斜率为-1,
解:(1)∵OM⊥l,∴直线l上的斜率为-1,
∴直线l上的方程为:$y-\frac{3}{2}=-(x-\frac{3}{2})$,即x+y-3=0.
(2)如图可知,对每个给定的点P,当PQ为圆O的切线时,∠OPQ最大,此时OQ⊥PQ,
若此时∠OPQ=30°,则$|{OP}|=2|{OQ}|=2\sqrt{2}$,故只需$|{OP}|≤2\sqrt{2}$即可,即$x_0^2+y_0^2≤8$,
又x0+y0-3=0⇒y0=3-x0,代入得:$x_0^2+(3-x_0^2)≤8⇒2x_0^2-6{x_0}+1≤0⇒\frac{{3-\sqrt{7}}}{2}≤{x_0}≤\frac{{3+\sqrt{7}}}{2}$.
(3)证明:据题意可求N(1,1),
∵N'是N关于x轴的对称点,∠ANN'=∠BNN',∴kAN=-kBN,设kAN=k,则kBN=-k,
则直线AN的方程为:y-1=k(x-1),直线BN的方程为:y-1=-k(x-1),
联立$\left\{{\begin{array}{l}{y=kx+1-k}\\{{x^2}+{y^2}=2}\end{array}}\right.$,消去y得:(1+k2)x2+2k(1-k)x+k2-2k-1=0,
∵${x_A}{x_N}=\frac{{{k^2}-2k-1}}{{1+{k^2}}}$,∴${x_A}=\frac{{{k^2}-2k-1}}{{1+{k^2}}}$,同理可求${x_B}=\frac{{{k^2}+2k-1}}{{1+{k^2}}}$,${k_{AB}}=\frac{{{y_B}-{y_A}}}{{{x_B}-{x_A}}}=\frac{{-({x_B}+{x_A})+2k}}{{{x_B}-{x_A}}}=\frac{4k}{3k}=1$,
故直线AB的斜率为定值1.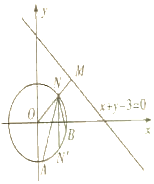
点评 本题考查直线方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )| A. |  | B. |  | C. | 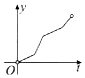 | D. | 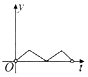 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com