
分析 (1)根据正弦函数的图象和性质可得f(x+a)=A,f(x)=-A,故a的最小值为f(x)的半周期.
(2)使用和角公式化简,利用三角函数的性质得出最大值.
解答 解:(1)∵f(x)的最大值为A,最小值为-A,f(x+a)-f(x)=2A,
∴f(x+a)=A,f(x)=-A,∴a的最小值为f(x)的半周期.
∵f(x)的周期T=π,∴a的最小值为$\frac{π}{2}$.
(2)f(x+$\frac{π}{6}$)=sin(2x+$\frac{π}{3}$+φ),f(x)=sin(2x+φ).
∴f(x+$\frac{π}{6}$)-f(x)=sin(2x+$\frac{π}{3}$+φ)-sin(2x+φ)=$\frac{1}{2}$sin(2x+φ)+$\frac{\sqrt{3}}{2}$cos(2x+φ)-sin(2x+φ)
=$\frac{\sqrt{3}}{2}$cos(2x+φ)-$\frac{1}{2}$sin(2x+φ)
=cos(2x+$\frac{π}{6}$+φ).
∴f(x+$\frac{π}{6}$)-f(x)的最大值为1.
故答案为$\frac{π}{2}$,1.
点评 本题考查了正弦函数的图象与性质,三角函数的恒等变换,属于中档题.


 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 36 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
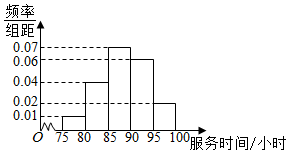 某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.
某市教育部门规定,高中学生三年在校期间必须参加不少于80小时的社区服务,教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段[75,80),[80,85),[85,90),[90,95),[95,100](单位:小时)进行统计,其频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
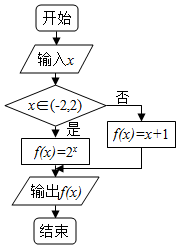
| A. | [0,2) | B. | [2,7] | C. | [2,4] | D. | [0,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com