
| A. | $\sqrt{10}$ | B. | $\sqrt{13}$ | C. | 3$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
分析 把已知等式变形,利用复数代数形式的乘除运算求得$\overline{z}$,再由$|\overline{z}|=|z|$求得答案.
解答 解:由($\overline{z}$+2i-3)(4+3i)=3-4i,
得$\overline{z}=\frac{3-4i}{4+3i}+3-2i=\frac{(3-4i)(4-3i)}{(4+3i)(4-3i)}+3-2i$=$\frac{-25i}{25}+3-2i=3-3i$,
∴$|\overline{z}|=|z|=\sqrt{{3}^{2}+(-3)^{2}}=3\sqrt{2}$.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查了共轭复数的概念,训练了复数模的求法,是基础题.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
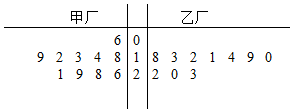 某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于17克时,该产品为优等品.现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量样品的质量指标值(单位:克)•如图是测量数据的茎叶图:
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于17克时,该产品为优等品.现在为了解甲、乙两厂产品的质量,从两厂生产的产品中分别随机抽取各10件样品,测量样品的质量指标值(单位:克)•如图是测量数据的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{25}$ | B. | $\frac{25}{7}$ | C. | $\frac{7}{25}$ | D. | $\frac{25}{17}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com