
已知圆C的圆心在坐标原点,且与直线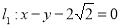 相切
相切
(1)求直线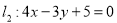 被圆C所截得的弦AB的长.
被圆C所截得的弦AB的长.
(2)过点G(1,3)作两条与圆C相切的直线,切点分别为M,N求直线MN的方程
(3)若与直线l1垂直的直线l与圆C交于不同的两点P,Q,若∠POQ为钝角,求直线l纵截距的取值范围.
(1)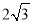 ;(2)
;(2)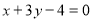 ;(3)
;(3)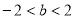 ,且
,且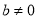
【解析】
试题分析:(1)先由点到直线距离公式求出原点到直线 的距离即为圆C的半径,再写出圆C的方程;(2)先求出以G为圆心|GM|的方程,圆G的方程与圆C方程相减就是其公共弦MN所在的直线方程;(3)先根据直线
的距离即为圆C的半径,再写出圆C的方程;(2)先求出以G为圆心|GM|的方程,圆G的方程与圆C方程相减就是其公共弦MN所在的直线方程;(3)先根据直线 的方程求出
的方程求出 的斜率,由直线
的斜率,由直线 ⊥
⊥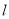 ,求出
,求出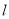 的斜率,设出
的斜率,设出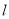 的斜截式方程,将直线
的斜截式方程,将直线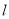 方程与圆C方程联立,消去y化为关于x的方程,设出
方程与圆C方程联立,消去y化为关于x的方程,设出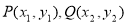 ,根据韦达定理将
,根据韦达定理将 ,
,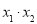 用直线
用直线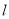 在y轴上截距b表示,由判别式大于0得到关于b的不等式,将∠POQ为钝角转化为
在y轴上截距b表示,由判别式大于0得到关于b的不等式,将∠POQ为钝角转化为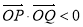 ,利用数量积的坐标运算,再列出关于b的不等式,这两个不等式联立就解出b的取值范围.
,利用数量积的坐标运算,再列出关于b的不等式,这两个不等式联立就解出b的取值范围.
试题解析:(1)由题意得:圆心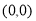 到直线
到直线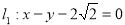 的距离为圆的半径,
的距离为圆的半径,
 ,所以圆
,所以圆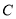 的标准方程为:
的标准方程为: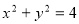 2分
2分
所以圆心到直线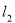 的距离
的距离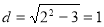 3分
3分

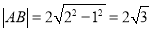 4分
4分
(2)因为点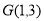 ,所以
,所以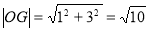 ,
,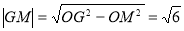
所以以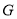 点为圆心,线段
点为圆心,线段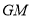 长为半径的圆
长为半径的圆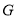 方程:
方程: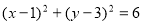 (1)
(1)
又圆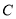 方程为:
方程为: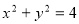 (2),由
(2),由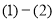 得直线
得直线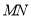 方程:
方程: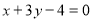 8分
8分
(3)设直线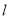 的方程为:
的方程为: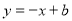
 联立
联立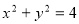 得:
得: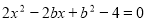 ,
,
设直线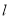 与圆的交点
与圆的交点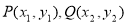 ,
,
由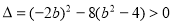 ,得
,得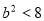 ,
,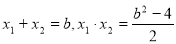 (3) 10分
(3) 10分
因为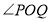 为钝角,所以
为钝角,所以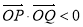 ,
,
即满足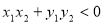 ,且
,且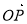 与
与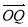 不是反向共线,
不是反向共线,
又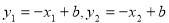 ,所以
,所以 (4)
(4)
由(3)(4)得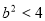 ,满足
,满足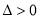 ,即
,即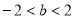 , 12分
, 12分
当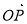 与
与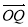 反向共线时,直线
反向共线时,直线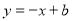 过原点,此时
过原点,此时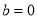 ,不满足题意,
,不满足题意,
故直线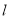 纵截距的取值范围是
纵截距的取值范围是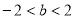 ,且
,且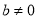 14分
14分
考点:点的直线的距离公司;圆的标准方程;圆与圆的位置关系;直线与圆的位置关系;设而不求思想


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源:2016届广东省清远市高一下学期期末考试数学试卷(解析版) 题型:填空题
某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本,若样本中的青年职工为7人,则样本容量为 _________ 人.
查看答案和解析>>
科目:高中数学 来源:2016届广东省清远市高一下学期期末考试数学试卷(解析版) 题型:选择题
为了从甲乙两人中选一人参加数学竞赛,老师将二人最近6次数学测试的分数进行统计,甲乙两人的平均成绩分别是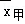 、
、 ,则下列说法正确的是( )
,则下列说法正确的是( )
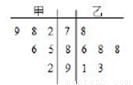
A.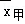 >
> ,乙比甲成绩稳定,应选乙参加比赛
,乙比甲成绩稳定,应选乙参加比赛
B.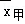 >
> ,甲比乙成绩稳定,应选甲参加比赛
,甲比乙成绩稳定,应选甲参加比赛
C.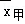 <
< ,甲比乙成绩稳定,应选甲参加比赛
,甲比乙成绩稳定,应选甲参加比赛
D.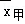 <
< ,乙比甲成绩稳定,应选乙参加比赛
,乙比甲成绩稳定,应选乙参加比赛
查看答案和解析>>
科目:高中数学 来源:2016届广东省深圳市南山区高一下学期期末统考数学试卷(解析版) 题型:解答题
已知函数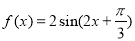
(1)求函数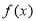 的最小正周期及单调递减区间;
的最小正周期及单调递减区间;
(2)若将函数的图像向右平移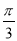 个单位,得到函数
个单位,得到函数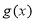 的图像,求
的图像,求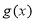 在区间
在区间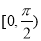 上的最大值和最小值,并求出相应的x的取值。
上的最大值和最小值,并求出相应的x的取值。
查看答案和解析>>
科目:高中数学 来源:2016届广东省梅州市高一上学期质检数学试卷(解析版) 题型:填空题
某中学为了解学生数学课程的学习情况,在3 000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测这3 000名学生在该次数学考试中成绩小于60分的学生数是_________
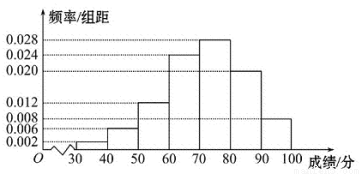
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com