
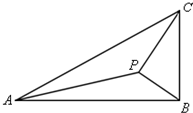
 如图,在△ABC中,∠ABC=90°,AB=$\sqrt{3}$,BC=1,P为△ABC内一点,∠BPC=90°.
如图,在△ABC中,∠ABC=90°,AB=$\sqrt{3}$,BC=1,P为△ABC内一点,∠BPC=90°.分析 (Ⅰ)由已知可求∠PBA=30°,在△PBA中,由余弦定理即可解得PA的值.
(Ⅱ)设∠PBA=α,由已知得,PB=sinα,在△PBA中,由正弦定理,同角三角函数基本关系式可得tanα的值,利用二倍角的正切函数公式即可计算得解.
解答 本小题满分(12分)
解:(Ⅰ)由已知得,∠PBC=60°,
∴∠PBA=30°,
在△PBA中,由余弦定理得PA2=$3+\frac{1}{4}-2×\sqrt{3}×\frac{1}{2}cos{30^o}$=$\frac{7}{4}$,
∴PA=$\frac{{\sqrt{7}}}{2}$…(5分)
(Ⅱ)设∠PBA=α,由已知得,PB=sinα,
在△PBA中,由正弦定理得,$\frac{{\sqrt{3}}}{{sin{{150}^o}}}=\frac{sinα}{{sin({{30}^o}-α)}}$,
化简得,$\sqrt{3}cosα=4sinα$,
∴tanα=$\frac{{\sqrt{3}}}{4}$,
∴$tan2α=\frac{2tanα}{{1-{{tan}^2}α}}=\frac{{8\sqrt{3}}}{13}$.…(12分)
点评 本题主要考查了余弦定理,正弦定理,同角三角函数基本关系式,二倍角的正切函数公式在解三角形中的应用,考查了转化思想和数形结合思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com