
分析 (Ⅰ)根据数列的递推公式公式得到数列{an}从第二项开始,以1为首项,以2为公比的等比数列,即可求出{an}的通项公式
(Ⅱ)根据对数的运算性质得到bn,再根据等差数列和等比数列的前n项和公式分组求和即可.
解答 解:(Ⅰ)∵Sn=an+1(n∈N*),
当n=1时,a1=S1=a2=1
∴Sn-1=an,
∴an=an+1-an,
∴an+1=2an,
∴数列{an}从第二项开始,以1为首项,以2为公比的等比数列,
∴an=2n-2,n≥2,
∴an=$\left\{\begin{array}{l}{1,n=1}\\{{2}^{n-2},n≥2}\end{array}\right.$,
(Ⅱ)当n=1时,b1=log2(2a1)=1,
当n≥2时,bn=log2(2an)=n-1,
∴Tn=a1+b1+a2+b2+a3+b3+an+bn=a1+b1+(a2+a3+…+an)+(b2+b3+…+bn)=2+$\frac{1×(1-{2}^{n-1})}{1-2}$+$\frac{(n-1)(1+n)}{2}$=2n-1+$\frac{{n}^{2}-1}{2}$+1=2n-1+$\frac{1}{2}$n2+$\frac{1}{2}$
点评 本题主要考查数列的递推公式和等比数列的通项公式,等差数列的通项公式,分组求和,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
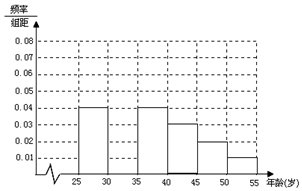 智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:
智能手机功能强大,许多人喜欢用手机看电视、看电影.某同学在暑假期间开展社会实践,对[25,55]岁的人群随机抽取1000人调查是否喜欢用手机看电视、看电影,对喜欢用手机看电视、看电影的称为“手机族”,得到如下各年龄段“手机族”人数频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{3}{2},-\frac{3}{2e}})$ | B. | $[{-\frac{3}{2e},-\frac{5}{{3{e^2}}}})$ | C. | $[{-\frac{3}{2},-\frac{5}{{3{e^2}}}})$ | D. | $[{-2e,-\frac{3}{2e}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com