
分析 (I)求导,由题意可知:2x2+4x-a=0在(-2,+∞)内有两个不相等实根,构造辅助函数,利用函数的性质,即可求得实数a的取值范围;
(II)由(I)可知,利用韦达定理,则$\frac{{f({x_1})}}{x_2}=\frac{{x_1^2-aln({x_1}+2)}}{x_2}={x_2}+\frac{4}{x_2}-2({x_2}+2)ln(-{x_2})+4$,构造辅助函数.利用导数求得函数的单调区间,则F(x)<F(1)=-1,即$\frac{{f({x_1})}}{x_2}<-1$.
解答 解:(Ⅰ)由题意,$f'(x)=2x-\frac{a}{x+2}(x>-2)$,-----------------(1分)
∵函数f(x)存在两个极值点x1,x2,且x1<x2,
∴关于x的方程$2x-\frac{a}{x+2}=0$,
即2x2+4x-a=0在(-2,+∞)内有两个不相等实根.--------------(2分)
令φ(x)=2x2+4x-a,
则$\left\{{\begin{array}{l}{△=16+8a>0}\\{φ(-2)>0}\end{array}}\right.$-----------------------------------------(3分)
解得-2<a<0.所以,实数a的取值范围(-2,0).-------------(4分)
(Ⅱ)证明:由(Ⅰ)知$\left\{{\begin{array}{l}{{x_1}{x_2}=-\frac{a}{2}}\\{{x_1}+{x_2}=-2}\\{-1<{x_2}<0}\end{array}}\right.$
∴$\frac{{f({x_1})}}{x_2}=\frac{{x_1^2-aln({x_1}+2)}}{x_2}={x_2}+\frac{4}{x_2}-2({x_2}+2)ln(-{x_2})+4$,---------(10分)
令-x2=x,则0<x<1,且$\frac{{f({x_1})}}{x_2}=-x-\frac{4}{x}+2(x-2)lnx+4$,
令$F(x)=-x-\frac{4}{x}+2(x-2)lnx+4(0<x<1)$,则------------------(11分)
$F'(x)=-1+\frac{4}{x^2}+2lnx+\frac{2(x-2)}{x}=\frac{4}{x^2}-\frac{4}{x}+2lnx+1(0<x<1)$------(12分)
∴$F''(x)=-\frac{8}{x^3}+\frac{4}{x^2}+\frac{2}{x}=\frac{{2({x^2}+2x-4)}}{x^3}$,
∵0<x<1,
∴F''(x)<0即F'(x)在(0,1)上是减函数,
∴F'(x)>F'(1)=1>0,
∴F(x)在(0,1)上是增函数,------------(13分)
∴F(x)<F(1)=-1,即$\frac{{f({x_1})}}{x_2}<-1$,
所以,$\frac{{f({x_1})}}{x_2}+1<0$.------------------------------------(14分)
点评 本题考查导数的综合应用,考查导数与函数单调性的关系,利用导数求函数的最值,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
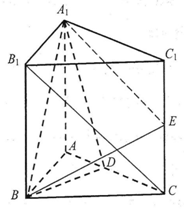 如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,D,E分别是AC,CC1的中点,$AB=BC=A{A_1}=\frac{{\sqrt{2}}}{2}AC$.
如图,侧棱垂直于底面的三棱柱ABC-A1B1C1中,D,E分别是AC,CC1的中点,$AB=BC=A{A_1}=\frac{{\sqrt{2}}}{2}AC$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 24 | C. | 20 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1∈M | B. | 2∈M | C. | (∁RB)⊆A | D. | B⊆A |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-2<x<1} | B. | {x|0<x<1} | C. | {x|x>2} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
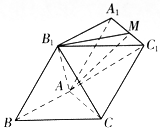 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,且侧面ABB1A1⊥底面ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com