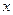练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知椭圆C的中心在原点，焦点在轴上，长轴长是短轴长的倍且经过点M
    （Ⅰ）求椭圆C的方程
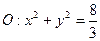    （Ⅱ）过圆上的任一点作圆的一条切线交椭圆C与A、B两点
    ①求证：
    ②求|AB|的取值范围
    解：（Ⅰ）设椭圆的长半轴长为，短轴长为，则由题意可得：
    ，所以椭圆的方程为；
    （Ⅱ）①当切线的斜率不存在时切线为与椭圆的两个交点为
    或满足
    当切线斜率存在时，可设的方程为.解方程组得,即, .   
    则△=,即
    ,



    ②由①可知：



    当时
    因为所以,
    所以,
    所以当且仅当时取”=”
    当时,.
    当AB的斜率不存在时, 两个交点为或,所以此时,
    综上, |AB |的取值范围为即:
    略
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分12分）
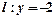    已知曲线C上任意一点M到点F（0，1）的距离比它到直线 的距离小1．
    （1）求曲线C的方程；
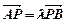    （2）过点P（2,2）的直线与曲线C交于A、B两点，设当△AOB的面积为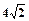时（O为坐标原点），求的值．
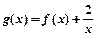    （3）若函数在[1，3]上是减函数，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本小题满分14分）
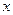    定长为3的线段AB两端点A、B分别在轴，轴上滑动，M在线段AB上，且
    （1）求点M的轨迹C的方程；
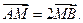
    （2）设过且不垂直于坐标轴的动直线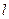交轨迹C于A、B两点，问：线段上
    是否存在一点D，使得以DA，DB为邻边的平行四边形为菱形？作出判断并证明。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （12分）从圆:外一动点向圆引一条切线，切点为，且(为坐标原点)，求的最小值和取得最小值时点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

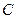    （本小题满分12分）已知椭圆的中心在原点，焦点在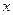轴上，点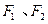分别是椭圆的左、右焦点，在直线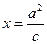(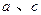分别为椭圆的长半轴和半焦距的长)上的点
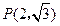    ，满足线段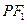的中垂线过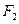点．过原点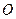且斜率均存在的直线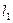、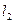互相垂直，且截椭圆所得的弦长分别为、．
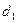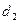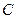    (Ⅰ)求椭圆的方程；
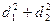    (Ⅱ)求的最小值及取得最小值时直线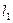、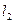的方程.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    双曲线P到左准线的距离是       

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

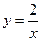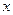    如图，双曲线(＞0）经过四边形OABC的顶点A、C，∠ABC＝90°，
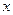    OC平分OA与轴正半轴的夹角，AB∥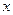轴，将△ABC沿AC翻折后得△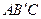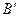，点
    落在OA上，则四边形OABC的面积是         .

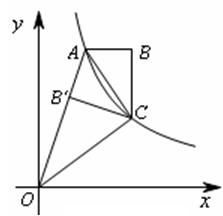
    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

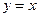    已知抛物线C的顶点在坐标原点，焦点在x轴上，直线与抛物线C相交
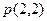    于A,B两点，若是AB的中点，则抛物线C的方程为_______________.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设为常数，若点是双曲线的一个焦点，则            。

    查看答案和解析>>

    同步练习册答案