
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.
如图,$OC=90km,∠AOB=\frac{2π}{3},∠OCD=θ$,点O处为一雷达站,测控范围为一个圆形区域(含边界),雷达开机时测控半径r随时间t变化函数为r=3t$\sqrt{t}$km,且半径增大到81km时不再变化.一架无人侦察机从C点处开始沿CD方向飞行,其飞行速度为15km/min.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
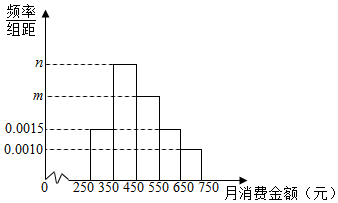
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2sin(x+$\frac{π}{6}$) | B. | f(x)=2sin(x+$\frac{π}{3}$) | C. | f(x)=2sin(2x+$\frac{π}{6}$) | D. | f(x)=2sin(2x+$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com