
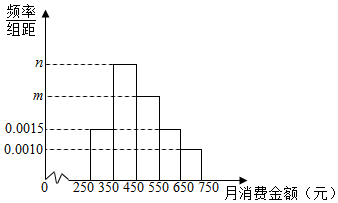
分析 (Ⅰ)由题意知 100(m+n)=0.6且2m=n+0.0015,由此能求出m,n的值,并求这100名学生月消费金额的样本平均数$\overline x$.
(Ⅱ)由题意从[350,450)中抽取7人,从[550,650)中抽取3人,随机变量X的取值所有可能取值有0,1,2,3,分别求出相应的概率,由此能求出随机变量X的分布列及随机变量X的数学期望E(X).
解答 解:(Ⅰ)由题意知 100(m+n)=0.6且2m=n+0.0015,
故m=0.0025,n=0.0035.…(3分)
所求平均数为:$\overline x=300×0.15+400×0.35+500×0.25+600×0.15+700×0.10=470$(元)…(5分)
(Ⅱ)由题意从[350,450)中抽取7人,从[550,650)中抽取3人…(7分)
随机变量X的取值所有可能取值有0,1,2,3,
$P(X=k)=\frac{{C_3^kC_7^{3-k}}}{{C_{10}^3}}(k=0,1,2,3)$…(9分)
所以,随机变量X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{35}{120}$ | $\frac{63}{120}$ | $\frac{21}{120}$ | $\frac{1}{120}$ |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sinx2<sin($\frac{5}{2}$-y) | B. | sinx2>sin(2-y) | C. | sin(2-x2)<siny | D. | sinx2<cos(y-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com