
分析 (Ⅰ)曲线C的极坐标方程可化为ρ2=2ρsinθ,由此能求出曲线C的直角坐标方程.
(Ⅱ)将直线l的参数方程化为直角坐标方程,求出M点的坐标,从而得到|MC|,再由|MN|≤|MC|+r,能求出MN的最大值.
解答 解:(Ⅰ)曲线C的极坐标方程可化为ρ2=2ρsinθ,…(2分)
又x2+y2=ρ2,x=ρcosθ,y=ρsinθ,
∴曲线C的直角坐标方程为x2+y2-2y=0.…(4分)
(Ⅱ)将直线l的参数方程化为直角坐标方程,得y=-$\frac{4}{3}(x-2)$.…(6分)
令y=0,得x=2,即M点的坐标为(2,0).
又曲线C为圆,圆C的圆心坐标为C(0,1),半径r=1,
∵直线l与x轴的交点是M,∴M(2,0),
∴|MC|=$\sqrt{4+1}$=$\sqrt{5}$,…(8分)
∵N是曲线C上一动点,∴|MN|≤|MC|+r=$\sqrt{5}+1$.
故MN的最大值为$\sqrt{5}+1$.…(10分)
点评 本题考查曲线的直角坐标方程的求法,考查线段长的最大值的求法,是中档题,解题时要认真审题,注意两点间距离公式的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{7π}{12}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{4}$,$\frac{1}{3}$] | B. | [$\frac{1}{4}$,$\frac{1}{3}$) | C. | [$\frac{1}{5}$,$\frac{1}{3}$) | D. | [$\frac{1}{5}$,$\frac{1}{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
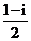 .
.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
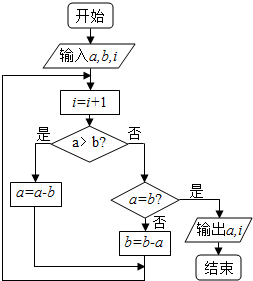 如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )
如图程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入a,b,i的值分别为6,8,0,则输出a和i的值分别为( )| A. | 0,3 | B. | 0,4 | C. | 2,3 | D. | 2,4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com