
分析 (Ⅰ)由ρ2=x2+y2,y=ρsinθ,x=ρcosθ,能求出C2的直角坐标方程.
(Ⅱ)曲线C1消去参数,得C1的直角坐标方程为$x+\sqrt{3}y+2=0$,求出圆心到直线C1的距离,由此能求出动点M到曲线C1的距离的最大值.
解答 解:(Ⅰ)$ρ=2\sqrt{2}cos({θ-\frac{π}{4}})=2({cos{\;}θ+sin{\;}θ})$,…(2分)
即ρ2=2(ρcosθ+ρsinθ),
∴x2+y2-2x-2y=0,
故C2的直角坐标方程为(x-1)2+(y-1)2=2.…(5分)
(Ⅱ)∵曲线C1的参数方程为$\left\{\begin{array}{l}{x=-2-\frac{\sqrt{3}t}{2}}\\{y=\frac{1}{2}t}\end{array}\right.$,
∴C1的直角坐标方程为$x+\sqrt{3}y+2=0$,
由(Ⅰ)知曲线C2是以(1,1)为圆心的圆,
且圆心到直线C1的距离$d=\frac{{\left|{1+\sqrt{3}+2}\right|}}{{\sqrt{{1^2}+{{({\sqrt{3}})}^2}}}}=\frac{{3+\sqrt{3}}}{2}$,…(8分)
∴动点M到曲线C1的距离的最大值为$\frac{{3+\sqrt{3}+2\sqrt{2}}}{2}$.…(10分)
点评 本题考查曲线的直角坐标方程的求法,考查点到曲线的距离的最大值的求法,是中档题,解题时要认真审题,注意点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 8 | C. | 10 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 点P在圆C上 | B. | 点P在圆C外 | C. | 点P在圆C内 | D. | 不能确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
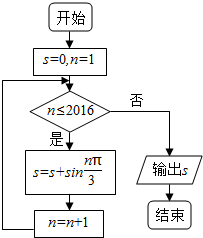
| A. | -$\sqrt{3}$ | B. | 0 | C. | $\sqrt{3}$ | D. | $336\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com