
分析 (1)利用二倍角公式和差角公式化简f(x),根据正弦函数的性质得出答案;
(2)求出f(x)的对称轴,得出x1与x2的关系,利用诱导公式化简即可得出答案.
解答 解:(1)f(x)=sinxcosx-$\sqrt{3}$cos2x+$\frac{\sqrt{3}}{2}$=$\frac{1}{2}$sin2x-$\sqrt{3}$•$\frac{1+cos2x}{2}$+$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x=sin(2x-$\frac{π}{3}$),
∴当2x-$\frac{π}{3}$=$\frac{π}{2}+2kπ$即x=$\frac{5π}{12}$+kπ,k∈Z时,f(x)取得最大值1.
(2)由(I)可知f(x)的图象关于直线x=$\frac{5π}{12}$对称,且f($\frac{5π}{12}$)=1,
∴x1+x2=$\frac{5π}{6}$,即x1=$\frac{5π}{6}$-x2,
∴cos(x1-x2)=cos($\frac{5π}{6}$-2x2)=cos($\frac{π}{2}$+$\frac{π}{3}$-2x2)=sin(2x2-$\frac{π}{3}$)=f(x2)=$\frac{2}{3}$.
点评 本题考查了三角函数的恒等变换,正弦函数的图象与性质,属于中档题.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
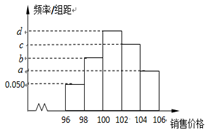 某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.
某企业市场调研部为调查新开发的产品定价与销量之间的关系,在某地区进行小范围差价试销,已知该产品定价区间为[96,106](单位:元/件),已知统计了600件产品的销售价格,其频率分布直方图如图所示,若各个小方形的高构成一个等差数列,则在这600件产品中,销售价格在区间[98,102)内的产品件数是135.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | $\frac{1}{9}$ | C. | $\frac{5}{3}$ | D. | -$\frac{5}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,-1} | B. | {-2} | C. | {-1,0,1} | D. | {0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1] | B. | (0,2-ln2) | C. | [1,2-ln2] | D. | [1,2-ln2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
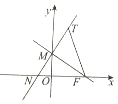 如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.
如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
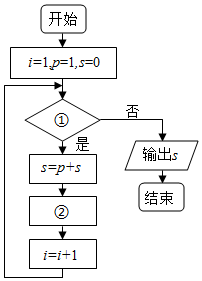 给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )| A. | i≤40?;p=p+i-1 | B. | i≤41?;p=p+i-1 | C. | i≤41?;p=p+i | D. | i≤40?;p=p+i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com