
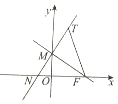
 如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.
如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.分析 (Ⅰ)设T(x,y),可知FM的斜率必存在,故设直线FN的方程为y=k(x-1),求出M(0,-k),N(-k2,0)),由T是点N关于直线FM的对称点,得T的坐标x,y满足$\left\{\begin{array}{l}{x={k}^{2}}\\{y=-2k}\end{array}\right.$.即可得曲线C的方程为y2=4x.
(Ⅱ)易得椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.假设存在直线l使A、F、Q是线段PB的四等分点,当直线l的斜率不存在或为0时,显然不满足题意.设直线l的方程为y=m(x-1)(m≠0).由图形可知,必有2AF=FB.联立方程,利用韦达定理解得m=$±2\sqrt{2}$,再分别验证即可.
解答 解:(Ⅰ)设T(x,y),可知FM的斜率必存在,故设直线FN的方程为y=k(x-1)
令x=0,得M(0,-k),∴当k≠0时,直线MN的方程为y+k=-$\frac{1}{k}x$.
令y=0,得N(-k2,0)),
∵T是点N关于直线FM的对称点∴T的坐标x,y满足$\left\{\begin{array}{l}{x={k}^{2}}\\{y=-2k}\end{array}\right.$.
消去k得y=4x,当k=0时得T(0,0).
曲线C的方程为y2=4x.
(Ⅱ)椭圆E的中心在坐标原点,F为其右焦点,且离心率为$\frac{1}{2}$,
∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$.
假设存在直线l使A、F、Q是线段PB的四等分点,
当直线l的斜率不存在或为0时,显然不满足题意.
设直线l的方程为y=m(x-1)(m≠0).
由图形可知,必有2AF=FB.
设A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=m(x-1)}\\{{y}^{2}=4x}\end{array}\right.$得my2-4y-4m=0;
△=16+16m2>0,∴${y}_{1}+{y}_{2}=\frac{4}{m}$,y1y2=-4;
∵2AF=FB.∴$\frac{{y}_{2}}{{y}_{1}}=-2$,
又∵$\frac{({y}_{1}+{y}_{2})^{2}}{{y}_{1}{y}_{2}}=\frac{{y}_{2}}{{y}_{1}}+2+\frac{{y}_{1}}{{y}_{2}}=-\frac{4}{{m}^{2}}$,
解得m=$±2\sqrt{2}$
①当m=2$\sqrt{2}$时,直线l的方程为y=2$\sqrt{2}$(x-1)
此时解得A($\frac{1}{2}$,-$\sqrt{2}$),B(2,2$\sqrt{2}$).
由$\left\{\begin{array}{l}{y=2\sqrt{2}(x-1)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,得P($\frac{2}{5}$,-$\frac{6\sqrt{2}}{5}$),Q($\frac{10}{7}$,$\frac{6\sqrt{2}}{7}$).
可得yB≠2yQ,∴点Q不是FB的中点,∴A、F、Q不是线段PB的四等分点.
同理m=-2$\sqrt{2}$时,也可得A、F、Q不是线段PB的四等分点.
综上不存在直线l使A、F、Q是线段PB的四等分点.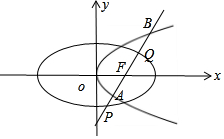
点评 本题考查了动点的轨迹方程的求解,直与椭圆的位置关系,方程思想,转化思想,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{π+2}$ | B. | $\frac{π}{π+4}$ | C. | $\frac{2}{π+1}$ | D. | $\frac{2}{π+2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | -i | C. | -1 | D. | i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{61}{60}$ | B. | -$\frac{122}{121}$ | C. | -$\frac{3}{4}$ | D. | -$\frac{90}{121}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com