
分析 (1)判断轨迹方程是椭圆,然后求解即可.
(2)直线l的方程可设为$y=kx+\frac{1}{3}$,设A(x1,y1),B(x2,y2),联立直线与椭圆方程,通过韦达定理,假设在y轴上是否存在定点Q(0,m),使以AB为直径的圆恒过这个点,利用$\overrightarrow{AQ}•\overrightarrow{BQ}=0$,求得m=-1.推出结果即可.
解答 解:(1)由题意得$|{M{F_1}}|+|{M{F_2}}|=|{M{F_1}}|+|{MP}|=|{{F_1}P}|=2\sqrt{2}>|{{F_1}{F_2}}|=2$,
∴点M的轨迹C为以F1,F2为焦点的椭圆∵$2a=2\sqrt{2},2c=2$,
∴点M的轨迹C的方程为$\frac{x^2}{2}+{y^2}=1$.
(2)直线l的方程可设为$y=kx+\frac{1}{3}$,设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}y=kx+\frac{1}{3}\\ \frac{x^2}{2}+{y^2}=1\end{array}\right.$可得9(1+2k2)x2+12kx-16=0.
由求根公式化简整理得${x_1}+{x_2}=-\frac{4k}{{3(1+2{k^2})}},{x_1}{x_2}=-\frac{16}{{9(1+2{k^2})}}$,
假设在y轴上是否存在定点Q(0,m),使以AB为直径的圆恒过这个点,则$\overrightarrow{AQ}⊥\overrightarrow{BQ}$即$\overrightarrow{AQ}•\overrightarrow{BQ}=0$.
∵$\overrightarrow{AQ}=(-{x_1},m-{y_1}),\overrightarrow{BQ}=(-{x_2},m-{y_2})$,
$\overrightarrow{AQ}•\overrightarrow{BQ}={x_1}{x_2}+(m-{y_1})(m-{y_2})={x_1}{x_2}+(m-k{x_1}-\frac{1}{3})(m-k{x_2}-\frac{1}{3})$=$(1+{k^2}){x_1}{x_2}+k(\frac{1}{3}-m)({x_1}+{x_2})+{m^2}-\frac{2m}{3}+\frac{1}{9}$=$-\frac{{16(1+{k^2})}}{{9(1+2{k^2})}}-\frac{{12{k^2}(\frac{1}{3}-m)}}{{9(1+2{k^2})}}+{m^2}-\frac{2m}{3}+\frac{1}{9}$=$\frac{{(18{m^2}-18){k^2}+(9{m^2}-6m-15)}}{{9(1+2{k^2})}}=0$.
∴$\left\{\begin{array}{l}18{m^2}-18=0\\ 9{m^2}-6m-15=0\end{array}\right.$求得m=-1.
因此,在y轴上存在定点Q(0,-1),使以AB为直径的圆恒过这个点.
点评 本题考查椭圆的方程的求法,直线与椭圆的位置关系的应用,考查计算能力以及转化思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
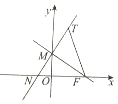 如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.
如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
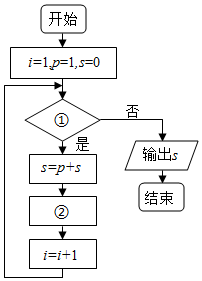 给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )
给出40个数:1,2,4,7,11,16,…,要计算这40个数的和,如图给出了该问题的程序框图,那么框图①处和执行框②处可分别填入( )| A. | i≤40?;p=p+i-1 | B. | i≤41?;p=p+i-1 | C. | i≤41?;p=p+i | D. | i≤40?;p=p+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | b>c>a | B. | b>a>c | C. | a>c>b | D. | a>b>c |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
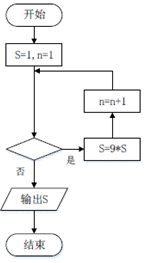 我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( )
我国古代算书《孙子算经》上有个有趣的问题“出门望九堤”:今有出门重九堤,堤有九木,木有九枝,枝有九巢,巢有九禽,禽有九雏,雏有九毛,毛有九色,问各几何?现在我们用右图所示的程序框图来解决这个问题,如果要使输出的结果为禽的数目,则在该框图中的判断框中应该填入的条件是( )| A. | S>10000? | B. | S<10000? | C. | n≥5 | D. | n≤6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
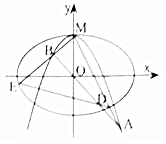 如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.
如图,抛物线C1:y=b-x2经过椭圆C2:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦点及上顶点M,过点M的两条互相垂直的直线l1,l2分别交抛物线于A,B两点,交椭圆于D,E两点,已知抛物线C1:y=b-x2与x轴所围成的区域面积为$\frac{4}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com