练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．棱长均为2的正四面体ABCD在平面α的一侧，Ω是ABCD在平面α内的正投影，设Ω的面积为S，则S的最大值为2，最小值为$\sqrt{2}$．

    分析 考虑两个特殊位置，即可得出结论．

    解答 解：由题意，设过AC与BD中点的平面α平行时，S最小，最小值为$\frac{1}{2}×2×\sqrt{3-1}$=$\sqrt{2}$，ABCD在平面α内的正投影构成等腰直角三角形（正方形的一半）时，S最大，最大值为$\frac{1}{2}×2×2$=2，
    故答案为2，$\sqrt{2}$．

    点评 本题考查平行投影及平行投影作图法，本题是一个计算投影面积的题目，注意解题过程中的投影图的变化情况，本题是一个中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

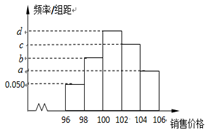    7．某企业市场调研部为调查新开发的产品定价与销量之间的关系，在某地区进行小范围差价试销，已知该产品定价区间为[96，106]（单位：元/件），已知统计了600件产品的销售价格，其频率分布直方图如图所示，若各个小方形的高构成一个等差数列，则在这600件产品中，销售价格在区间[98，102）内的产品件数是135．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

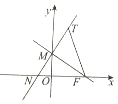    8．如图，在平面直角坐标中，过F（1，0）的直线FM与y轴交于点M，直线MN与直线FM垂直，且与x轴交于点N，T是点N关于直线FM的对称点．
    （1）点T的轨迹为曲线C，求曲线C的方程；
    （2）椭圆E的中心在坐标原点，F为其右焦点，且离心率为$\frac{1}{2}$，过点F的直线l与曲线C交于A、B两点，与椭圆交于P、Q两点，请问：是否存在直线使A、F、Q是线段PB的四等分点？若存在，求出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知向量$\overrightarrow{OA}=（{3，1}），\overrightarrow{OB}=（{-1，3}）$，$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}（{m＞0，n＞0}）$，若m+n=1，则$|{\overrightarrow{OC}}$|的最小值为（　　）
    A．$\frac{{\sqrt{5}}}{2}$B．$\frac{{\sqrt{10}}}{2}$C．$\sqrt{5}$D．$\sqrt{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．角α的终边经过的一点P的坐标是（-$\sqrt{3}$，a），则“|a|=1”的充要条件是（　　）
    A．$sinα=\frac{1}{2}$B．$cosα=-\frac{{\sqrt{3}}}{2}$C．$tanα=-\frac{{\sqrt{3}}}{3}$D．$|PO|=\sqrt{3}+1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知等比数列{an}满足a1=$\frac{1}{2}，{a_2}{a_8}=2{a_5}$+3，则a9=（　　）
    A．$-\frac{1}{2}$B．$\frac{9}{8}$C．648D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

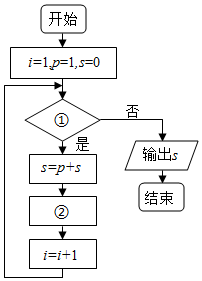    9．给出40个数：1，2，4，7，11，16，…，要计算这40个数的和，如图给出了该问题的程序框图，那么框图①处和执行框②处可分别填入（　　）
    A．i≤40？；p=p+i-1B．i≤41？；p=p+i-1C．i≤41？；p=p+iD．i≤40？；p=p+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．设函数f（x）=$\left\{\begin{array}{l}{lo{g}_{0.2}x，x∈（1，+∞）}\\{2-2x，x∈（-∞，1]}\end{array}\right.$，若a=f（20.3），b=f（log0.32），c=f（log32），则a、b、c的大小关系是（　　）
    A．b＞c＞aB．b＞a＞cC．a＞c＞bD．a＞b＞c

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知2a+2b=2c，则a+b-2c的最大值等于（　　）
    A．-2B．-1C．$\frac{1}{4}$D．-$\frac{1}{4}$

    查看答案和解析>>

    同步练习册答案