
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,长轴长为4,且过点
,长轴长为4,且过点![]() .
.
(1)求椭圆C的方程;
(2)过![]() 的直线l交椭圆C于
的直线l交椭圆C于![]() 两点,过A作x轴的垂线交椭圆C与另一点Q(Q不与
两点,过A作x轴的垂线交椭圆C与另一点Q(Q不与![]() 重合).设
重合).设![]() 的外心为G,求证
的外心为G,求证![]() 为定值.
为定值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在单位圆O:x2+y2=1上任取一点P(x,y),圆O与x轴正向的交点是A,设将OA绕原点O旋转到OP所成的角为θ,记x,y关于θ的表达式分别为x=f(θ),y=g(θ),则下列说法正确的是( )
A.x=f(θ)是偶函数,y=g(θ)是奇函数
B.x=f(θ)在![]() 为增函数,y=g(θ)在
为增函数,y=g(θ)在![]() 为减函数
为减函数
C.f(θ)+g(θ)≥1对于![]() 恒成立
恒成立
D.函数t=2f(θ)+g(2θ)的最大值为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,直线
,直线![]() ,过动点
,过动点![]() 作
作![]() 于点
于点![]() ,
,![]() 的平分线交
的平分线交![]() 轴于点
轴于点![]() ,且
,且![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
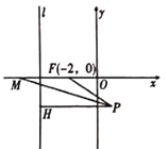
(1)求曲线![]() 的方程;
的方程;
(2)过点![]() 作两条直线,分别交曲线
作两条直线,分别交曲线![]() 于
于![]() 两点(异于
两点(异于![]() 点).当直线
点).当直线![]() 的斜率之和为2时,直线
的斜率之和为2时,直线![]() 是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
是否恒过定点?若是,求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.
(1)求椭圆C的标准方程;
(2)设F为椭圆C的左焦点,T为直线![]() 上任意一点,过F作TF的垂线交椭圆C于点P,Q.
上任意一点,过F作TF的垂线交椭圆C于点P,Q.
(i)证明:OT平分线段PQ(其中O为坐标原点);
(ii)当![]() 最小时,求点T的坐标.
最小时,求点T的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校开展学生社会法治服务项目,共设置了文明交通,社区服务,环保宣传和中国传统文化宣讲四个项目,现有该校的甲、乙、丙、丁4名学生,每名学生必须且只能选择1项.
(1)求恰有2个项目没有被这4名学生选择的概率;
(2)求“环保宣传”被这4名学生选择的人数![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 有两个不同的极值点
有两个不同的极值点![]() .
.
(1)求![]() 的取值范围.
的取值范围.
(2)求![]() 的极大值与极小值之和的取值范围.
的极大值与极小值之和的取值范围.
(3)若![]() ,则
,则![]() 是否有最小值?若有,求出最小值;若没有,说明理由.
是否有最小值?若有,求出最小值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为抛物线
为抛物线![]() 上的一点,
上的一点,![]() ,
,![]() 为抛物线上异于点
为抛物线上异于点![]() 的两点,且直线
的两点,且直线![]() 的斜率与直线
的斜率与直线![]() 的斜率互为相反数.
的斜率互为相反数.
(1)求直线![]() 的斜率;
的斜率;
(2)设直线![]() 过点
过点![]() 并交抛物线于
并交抛物线于![]() ,
,![]() 两点,且
两点,且![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,试探究
,试探究![]() 与
与![]() 的夹角是否为定值,若是则求出定值,若不是,说明理由.
的夹角是否为定值,若是则求出定值,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A,B的坐标分别是(![]() ,0),(
,0),(![]() ,0),动点M(x,y)满足直线AM和BM的斜率之积为﹣3,记M的轨迹为曲线E.
,0),动点M(x,y)满足直线AM和BM的斜率之积为﹣3,记M的轨迹为曲线E.
(1)求曲线E的方程;
(2)直线y=kx+m与曲线E相交于P,Q两点,若曲线E上存在点R,使得四边形OPRQ为平行四边形(其中O为坐标原点),求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是以
是以![]() 为直径的圆上一点,
为直径的圆上一点,![]() ,等腰梯形
,等腰梯形![]() 所在的平面垂直于⊙
所在的平面垂直于⊙![]() 所在的平面,且
所在的平面,且![]() .
.
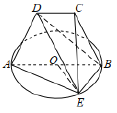
(1)求![]() 与
与![]() 所成的角;
所成的角;
(2)若异面直线![]() 和
和![]() 所成的角为
所成的角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com