
分析 (1)设等差数列{an}的公差为d,由首项a1=-1,可得a1+a2+a3=3d-3.数列{bn}满足bn=($\frac{1}{2}$)${\;}^{{a}_{n}}$,且b1b2b3=$\frac{1}{64}$.可得$(\frac{1}{2})^{{a}_{1}+{a}_{2}+{a}_{3}}$=$(\frac{1}{2})^{3d-3}$=$(\frac{1}{2})^{6}$,解得d即可得出.
(2)cn=(-1)n$\frac{6n-5}{{a}_{n}{a}_{n+1}}$=(-1)n$(\frac{1}{3n-4}+\frac{1}{3n-1})$,对n分类讨论即可得出.
解答 解:(1)设等差数列{an}的公差为d,∵首项a1=-1,∴a1+a2+a3=-3+$\frac{3×2}{2}d$=3d-3.
数列{bn}满足bn=($\frac{1}{2}$)${\;}^{{a}_{n}}$,且b1b2b3=$\frac{1}{64}$.
∴$(\frac{1}{2})^{{a}_{1}+{a}_{2}+{a}_{3}}$=$(\frac{1}{2})^{3d-3}$=$(\frac{1}{2})^{6}$,∴3d-3=6,解得d=3.
∴an=-1+3(n-1)=3n-4.
(2)cn=(-1)n$\frac{6n-5}{{a}_{n}{a}_{n+1}}$=(-1)n$(\frac{1}{3n-4}+\frac{1}{3n-1})$,
∴当n为偶数时,
数列{cn}的前n项的和Tn=$-(-1+\frac{1}{2})$+$(\frac{1}{2}+\frac{1}{5})$-…-$(\frac{1}{3n-7}+\frac{1}{3n-4})$+$(\frac{1}{3n-4}+\frac{1}{3n-1})$
=1+$\frac{1}{3n-1}$=$\frac{3n}{3n-1}$.
当n为奇数时,数列{cn}的前n项的和Tn=Tn-1-$(\frac{1}{3n-4}+\frac{1}{3n-1})$
=$\frac{3(n-1)}{3(n-1)-1}$-$(\frac{1}{3n-4}+\frac{1}{3n-1})$=$\frac{3n-2}{3n-1}$.
∴Tn=$\left\{\begin{array}{l}{\frac{3n}{3n-1},n为偶数}\\{\frac{3n-2}{3n-1},n为奇数}\end{array}\right.$.
点评 本题考查了等差数列的通项公式、指数幂的运算性质、“裂项求和”方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
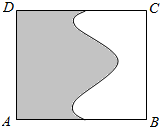 如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.
如图面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD投掷1000个点,落在矩形ABCD的非阴影部分中的点数为400个,试估计阴影部分的面积为2.4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,4) | B. | (1,2) | C. | -7 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com