
 (1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;
(1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;分析 (1)令3x-$\frac{π}{4}$≠$\frac{π}{2}$+kπ解出;
(2)令$\left\{\begin{array}{l}{sinx>0}\\{cosx-\frac{1}{2}≥0}\end{array}\right.$解出;
(3)利用图象依次求出A,ω,φ,再计算f(0).
解答 解:(1)由3x-$\frac{π}{4}$≠$\frac{π}{2}$+kπ得x≠$\frac{π}{4}$+$\frac{kπ}{3}$,
∴f(x)=tan(3x-$\frac{π}{4}$)的定义域为{x|x≠$\frac{π}{4}$+$\frac{kπ}{3}$,k∈Z}.
(2)由sinx>0得2kπ<x<2kπ+π,
由cosx$-\frac{1}{2}$≥0得cosx$≥\frac{1}{2}$,∴-$\frac{π}{3}$+2kπ≤x≤$\frac{π}{3}$+2kπ,
(2kπ,2kπ+π)∩[-$\frac{π}{3}$+2kπ,$\frac{π}{3}$+2kπ]=(2kπ,$\frac{π}{3}$+2kπ].
∴求函数y=lg(sinx)+$\sqrt{cosx-\frac{1}{2}}$的定义域为{x|2kπ<x≤$\frac{π}{3}$+2kπ,k∈Z}.
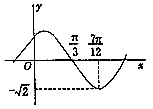
(3)由f(x)得图象可知-A=-$\sqrt{2}$,即A=$\sqrt{2}$,
由图象可知f(x)的周期T=4($\frac{7π}{12}-$$\frac{π}{3}$)=π,即$\frac{2π}{ω}$=π,∴ω=2.
又f($\frac{7π}{12}$)=$\sqrt{2}$sin($\frac{7π}{6}$+φ)=-$\sqrt{2}$,∴sin($\frac{7π}{6}$+φ)=-1,
∴$\frac{7π}{6}$+φ=-$\frac{π}{2}$+2kπ,解得φ=-$\frac{5π}{3}$+2kπ,
∴f(0)=$\sqrt{2}$sinφ=$\sqrt{2}$sin(-$\frac{5π}{3}$)=-$\frac{\sqrt{6}}{2}$.
点评 本题考查了三角函数的图象与性质,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | (0,4) | C. | [3,+∞) | D. | [4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 13 | C. | 9 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ②③④ | C. | ①②④ | D. | ①② |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 125 | B. | 5 625 | C. | 8 125 | D. | 0 625 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com