
分析 (1)直接由f(x1)-f(x2)≤0求得a的取值范围;
(2)若f(x)是周期函数,记其周期为Tk,任取x0∈R,则有f(x0)=f(x0+Tk),证明对任意x∈[x0,x0+Tk],f(x0)≤f(x)≤f(x0+Tk),可得f(x0)=f(x0+nTk),n∈Z,再由…∪[x0-3Tk,x0-2Tk]∪[x0-2Tk,x0-Tk]∪[x0-Tk,x0]∪[x0,x0+Tk]∪[x0+Tk,x0+2Tk]∪…=R,可得对任意x∈R,f(x)=f(x0)=C,为常数;
(3)分充分性及必要性证明.类似(2)证明充分性;必要性先证明f(x)符号不变,然后分类证明.
解答 (1)解:由f(x1)≤f(x2),得f(x1)-f(x2)=$a({{x}_{1}}^{3}-{{x}_{2}}^{3})≤0$,
∵x1<x2,∴${{x}_{1}}^{3}-{{x}_{2}}^{3}$<0,得a≥0.
故a的范围是[0,+∞);
(2)证明:若f(x)是周期函数,记其周期为Tk,任取x0∈R,则有
f(x0)=f(x0+Tk),
由题意,对任意x∈[x0,x0+Tk],f(x0)≤f(x)≤f(x0+Tk),
∴f(x0)=f(x)=f(x0+Tk).
又∵f(x0)=f(x0+nTk),n∈Z,并且
…∪[x0-3Tk,x0-2Tk]∪[x0-2Tk,x0-Tk]∪[x0-Tk,x0]∪[x0,x0+Tk]∪[x0+Tk,x0+2Tk]∪…=R,
∴对任意x∈R,f(x)=f(x0)=C,为常数;
(3)证明:充分性:若f(x)是常值函数,记f(x)=c1,设g(x)的一个周期为Tg,则
h(x)=c1•g(x),则对任意x0∈R,
h(x0+Tg)=c1•g(x0+Tg)=c1•g(x0)=h(x0),
故h(x)是周期函数;
必要性:若h(x)是周期函数,记其一个周期为Th,首先证明f(x)符号不变.
①设集合A={x|g(x)=m},若存在x0∈R,使得f(x0)=0,则
h(x0)=0,且对任意k∈Z,有h(x0+kTh)=0,
∵g(x)>0,∴f(x0+kTh)=0,即对任意x∈[x0+kTh,x0+(k+1)Th],k∈Z,f(x)=0恒成立,
∴f(x)=0是常值函数;
②若存在x1,x2,使得f(x1)>0,且f(x2)<0,则由题意可知,
x1>x2,那么必然存在正整数N1,使得x2+N1Tk>x1,
∴f(x2+N1Tk)>f(x1)>0,且h(x2+N1Tk)=h(x2).
又h(x2)=g(x2)f(x2)<0,而
h(x2+N1Tk)=g(x2+N1Tk)f(x2+N1Tk)>0≠h(x2),矛盾.
综上,f(x)=0或f(x)>0或f(x)<0恒成立.
1°、若f(x)>0恒成立,
任取x0∈A,则必存在N2∈N,使得x0-N2Th≤x0-Tg,
即[x0-Tg,x0]⊆[x0-N2Th,x0],
∵…∪[x0-3Tk,x0-2Tk]∪[x0-2Tk,x0-Tk]∪[x0-Tk,x0]∪[x0,x0+Tk]∪[x0+Tk,x0+2Tk]∪…=R,
∴…∪[x0-2N2Th,x0-N2Th]∪[x0-N2Th,x0]∪[x0,x0+N2Th]∪[x0+N2Th,x0+2N2Th]∪…=R.
h(x0)=g(x0)•f(x0)=h(x0-N2Th)=g(x0-N2Th)•f(x0-N2Th),
∵g(x0)=M≥g(x0-N2Th)>0,f(x0)≥f(x0-N2Th)>0.
因此若h(x0)=h(x0-N2Th),必有g(x0)=M=g(x0-N2Th),且f(x0)=f(x0-N2Th)=c.
而由(2)证明可知,对任意x∈R,f(x)=f(x0)=C,为常数.
2°、若f(x)<0恒成立,
任取x0∈A,则必存在N3∈N,使得x0+N3Th≥x0+Tg.
即[x0,x0+Tg]⊆[x0,x0+N3Tg],
∵…∪[x0-3Tk,x0-2Tk]∪[x0-2Tk,x0-Tk]∪[x0-Tk,x0]∪[x0,x0+Tk]∪[x0+Tk,x0+2Tk]∪…=R,
∴…∪[x0-2N3Th,x0-N3Th]∪[x0-N3Th,x0]∪[x0,x0+N3Th]∪[x0+N3Th,x0+2N3Th]∪…=R.
h(x0)=g(x0)•f(x0)=h(x0+N3Th)=g(x0+N3Th)•f(x0+N3Th).
∵g(x0)=M≥g(x0+N3Th)>0,f(x0)≤f(x0+N3Th)<0.
因此若h(x0)=h(x0+N3Th),
必有g(x0)=M=g(x0+N3Th),且f(x0)=f(x0+N3Th)=c,
而由(2)证明可知,对任意x∈R,f(x)=f(x0)=C,为常数.
综上,必要性得证.
点评 本题考查抽象函数及其应用,考查逻辑思维能力与理论运算能力考查分类讨论的数学思想方法,题目设置难度过大.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
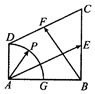 在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )
在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在$\widehat{DG}$上运动(如图).若$\overrightarrow{AP}$=λ$\overrightarrow{AE}$+μ$\overrightarrow{BF}$,其中λ,μ∈R,则6λ+μ的取值范围是( )| A. | [1,$\sqrt{2}$] | B. | [$\sqrt{2}$,2$\sqrt{2}$] | C. | [2,2$\sqrt{2}$] | D. | [1,2$\sqrt{2}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,e) | B. | (1,+∞) | C. | (1,e) | D. | (e,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 (1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;
(1)求f(x)=tan(3x-$\frac{π}{4}$)的定义域;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com