Question

13．从某校高三1200名学生中随机抽取40名，将他们一次数学模拟成绩绘制成频率分布直方图（如图）（满分为150分，成绩均为不低于80分整数），分为7段：[80，90），[90，100），[100，110），[110，120），[120，130），[130，140），[140，150]．

（1）求图中的实数a的值，并估计该高三学生这次成绩在120分以上的人数；
（2）在随机抽取的40名学生中，从成绩在[90，100）与[140，150]两个分数段内随机抽取两名学生，求这两名学生的成绩之差的绝对值标不大于10的概率．

Answer 1

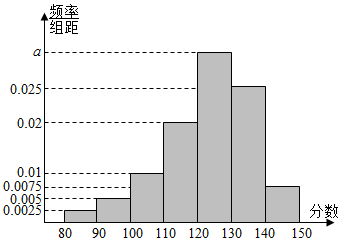
分析 （1）由频率分布直方图中频率之和为1，能求出a，估计该校成绩在120分以上人数即可；
（2）根据概率公式计算即可．

解答 解：（1）由0.025+0.05+0.075+0.1+0.2+0.25+10a=1，得a=0.03成绩在120分以上的人频率为0.3+0.25+0.075=0.625，估计该校成绩在120分以上人数为1200×0.625=750人，
（2）成绩在[90，100）与[140，150]两个分数段内学生人数分别为2人和3人，从中抽出2人的基本事件总数为10种，其中这两名学生的成绩之差的绝对值不大于10的事件数为4，所求概率为p=$\frac{4}{10}$=$\frac{2}{5}$．

点评 本小题主要考查频率、频数、统计和概率等知识，考查数形结合、化归与转化的数学思想方法，以及运算求解能力．