
已知常数 ,函数
,函数 .
.
(1)讨论 在区间
在区间 上的单调性;
上的单调性;
(2)若 存在两个极值点
存在两个极值点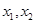 ,且
,且 ,求
,求 的取值范围.
的取值范围.
(1)详见解析 (2)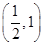
解析试题分析:(1)首先对函数 求导并化简得到导函数
求导并化简得到导函数 ,导函数的分母恒大于0,分子为含参的二次函数,故讨论分子的符号,确定导函数符号得到原函数的单调性,即分
,导函数的分母恒大于0,分子为含参的二次函数,故讨论分子的符号,确定导函数符号得到原函数的单调性,即分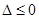 和
和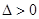 得到导函数分子大于0和小于0的解集进而得到函数的单调性.
得到导函数分子大于0和小于0的解集进而得到函数的单调性.
(2)利用第(1)可得到当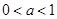 时,导数等于0有两个根,根据题意即为两个极值点,首先导函数等于0的两个根必须在原函数
时,导数等于0有两个根,根据题意即为两个极值点,首先导函数等于0的两个根必须在原函数 的可行域内,把
的可行域内,把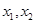 关于
关于 的表达式带入
的表达式带入 ,得到关于
,得到关于 的不等式,然后利用导函数讨论
的不等式,然后利用导函数讨论 的取值范围使得
的取值范围使得 成立.即可解决该问题.
成立.即可解决该问题.
(1)对函数 求导可得
求导可得
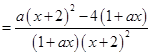
 ,因为
,因为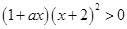 ,所以当
,所以当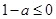 时,即
时,即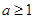 时,
时,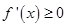 恒成立,则函数
恒成立,则函数 在
在 单调递增,当
单调递增,当 时,
时,  ,则函数
,则函数 在区间
在区间 单调递减,在
单调递减,在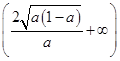 单调递增的.
单调递增的.
(2)解:(1)对函数 求导可得
求导可得
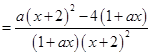
 ,因为
,因为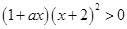 ,所以当
,所以当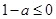 时,即
时,即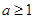 时,
时,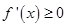 恒成立,则函数
恒成立,则函数 在
在 单调递增,当
单调递增,当 时,
时,  ,则函数
,则函数 在区间
在区间 单调递减,在
单调递减,在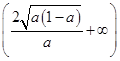 单调递增的.
单调递增的.
(2)函数 的定义域为
的定义域为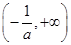 ,由(1)可得当
,由(1)可得当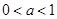 时,
时, ,则
,则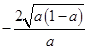
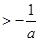

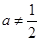 ,即
,即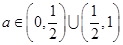 ,则
,则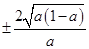 为函数
为函数 的两个极值点,代入
的两个极值点,代入 可得
可得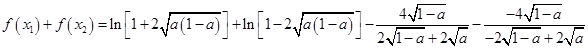
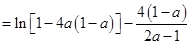 =
=
令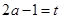 ,令
,令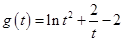 ,由
,由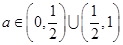 知: 当
知: 当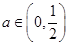 时,
时,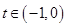 , 当
, 当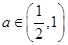 时,
时,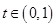 ,
,
当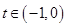 时,
时,

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2 ,上、下两边各空2dm,左、右两边各空1dm。如何设计海报的尺寸,才能使四周空白面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数
(1)若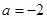 ,求证:函数
,求证:函数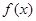 在(1,+∞)上是增函数;
在(1,+∞)上是增函数;
(2)当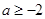 时,求函数
时,求函数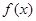 在[1,e]上的最小值及相应的x值;
在[1,e]上的最小值及相应的x值;
(3)若存在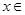 [l,e],使得
[l,e],使得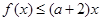 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=ax+x2-xln a(a>0,a≠1).
(1)求函数f(x)在点(0,f(0))处的切线方程;
(2)求函数f(x)的单调增区间;
(3)若存在x1,x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1(e是自然对数的底数),求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2-1与函数g(x)=aln x(a≠0).
(1)若f(x),g(x)的图像在点(1,0)处有公共的切线,求实数a的值;
(2)设F(x)=f(x)-2g(x),求函数F(x)的极值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com