
给定椭圆C: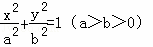 ,称圆心在坐标原点O,半径为
,称圆心在坐标原点O,半径为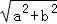 的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是
的圆是椭圆C的“伴随圆”,已知椭圆C的两个焦点分别是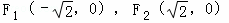 .
.
(1)若椭圆C上一动点M1满足|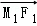 |+|
|+|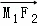 |=4,求椭圆C及其“伴随圆”的方程;
|=4,求椭圆C及其“伴随圆”的方程;
(2)在(1)的条件下,过点P(0,t)(t<0)作直线l与椭圆C只有一个交点,且截椭圆C的“伴随圆”所得弦长为2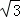 ,求P点的坐标;
,求P点的坐标;
(3)已知m+n=﹣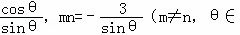 (0,π)),是否存在a,b,使椭圆C的“伴随圆”上的点到过两点(m,m2),(n,n2)的直线的最短距离
(0,π)),是否存在a,b,使椭圆C的“伴随圆”上的点到过两点(m,m2),(n,n2)的直线的最短距离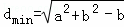 .若存在,求出a,b的值;若不存在,请说明理由.
.若存在,求出a,b的值;若不存在,请说明理由.
【解析】(1)由题意,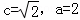 ,∴
,∴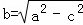 =
=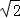 ,所以椭圆C的方程为
,所以椭圆C的方程为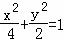 .
.
其“伴随圆”的方程为x2+y2=6;
(2)设直线l的方程为y=kx+t,代入椭圆方程为(2k2+1)x2+4tkx+2t2﹣4=0
∴由△=(4tk)2﹣8(2k2+1)(t2﹣2)=0得t2=4k2+2①,
由直线l截椭圆C的“伴随圆”所得弦长为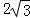 ,可得
,可得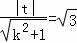 ,即t2=3(k2+1)②
,即t2=3(k2+1)②
由①②可得t2=6.
∵t<0,∴t=﹣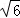 ,∴P(0,﹣
,∴P(0,﹣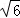 );
);
(3)过两点(m,m2),(n,n2)的直线的方程为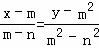 ,∴y=(m+n)x﹣mn,
,∴y=(m+n)x﹣mn,
∵m+n=﹣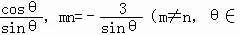 (0,π)),
(0,π)),
∴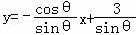 ,得xcosθ+ysinθ﹣3=0,
,得xcosθ+ysinθ﹣3=0,
∴由于圆心(0,0)到直线xcosθ+ysinθ﹣3=0的距离为d=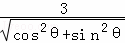 =3.
=3.
当a2+b2≥9时,dmin=0,但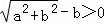 ,所以,等式不能成立;
,所以,等式不能成立;
当a2+b2<9时,dmin=3﹣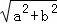 ,由3﹣
,由3﹣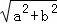 =
=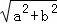 ﹣b得9+6b+b2=4a2+4b2.
﹣b得9+6b+b2=4a2+4b2.
因为a2=b2+2,所以7b2﹣6b﹣1=0,
∴(7b+1)(b﹣1)=0,∴b=1,a=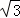 .
.


科目:高中数学 来源: 题型:
若将函数f(x)=x5表示为f(x)=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,其中a0,a1,a2,…a5为实数,则a3= _________ .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={f(x)|f2(x)﹣f2(y)=f(x+y)•f(x﹣y),x、y∈R},有下列命题:
①若f(x)=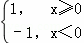 ,则f(x)∈A;
,则f(x)∈A;
②若f(x)=kx,则f(x)∈A;
③若f(x)∈A,则y=f(x)可为奇函数;
④若f(x)∈A,则对任意不等实数x1,x2,总有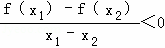 成立.
成立.
其中所有正确命题的序号是 ______ .(填上所有正确命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com