
设命题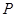 :函数
:函数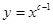 在
在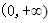 上为减函数, 命题
上为减函数, 命题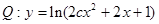 的值域为
的值域为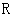 ,命题
,命题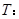 函数
函数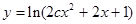 定义域为
定义域为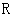
(1)若命题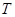 为真命题,求
为真命题,求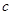 的取值范围。
的取值范围。
(2)若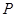 或
或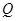 为真命题,
为真命题,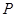 且
且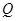 为假命题,求
为假命题,求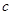 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
已知函数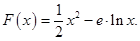
(I)求函数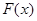 的极值;
的极值;
(II)对于函数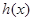 和
和 定义域内的任意实数
定义域内的任意实数 ,若存在常数
,若存在常数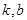 ,使得不等式
,使得不等式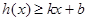 和
和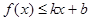 都成立,则称直线
都成立,则称直线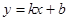 是函数
是函数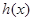 和
和 的“分界线”.
的“分界线”.
设函数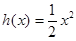 ,
,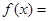
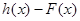 ,试问函数
,试问函数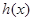 和
和 是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
是否存在“分界线”?若存在,求出“分界线”的方程.若不存在请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数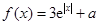 (
(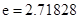 是自然对数的底数)的最小值为
是自然对数的底数)的最小值为 .
.
(Ⅰ)求实数 的值;
的值;
(Ⅱ)已知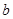
 且
且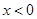 ,试解关于
,试解关于 的不等式
的不等式 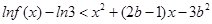 ;
;
(Ⅲ)已知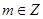 且
且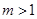 .若存在实数
.若存在实数 ,使得对任意的
,使得对任意的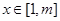 ,都有
,都有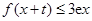 ,试求
,试求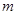 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
美国华尔街的次贷危机引起的金融风暴席卷全球,低迷的市场造成产品销售越来越难,为此某厂家举行大型的促销活动,经测算该产品的销售量P万件(生产量与销售量相等)与促销费用 万元满足
万元满足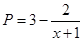 ,已知生产该产品还需投入成本
,已知生产该产品还需投入成本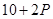 万元(不含促销费用),产品的销售价格定为
万元(不含促销费用),产品的销售价格定为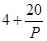 元.
元.
(Ⅰ)将该产品的利润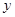 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(Ⅱ)促销费用投入多少万元时,厂家的利润最大。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com