
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
【答案】(Ⅰ)4 ;(Ⅱ) ![]() ;(Ⅲ)本题为开放问题,答案不唯一.
;(Ⅲ)本题为开放问题,答案不唯一.
【解析】试题分析:(1)将自变量的取值情况写出来,根据众数的概念可得结果;(2)将题目中满足从满足![]() 的测试中随机抽取两次的事件次数数出来,满足品牌A的测试结果恰好有一次大于品牌B的测试结果的次数数出来,两个数据作比即可;(3)可以从题目中的条件中,从多个角度下结论,只要解释的有道理均可得分。
的测试中随机抽取两次的事件次数数出来,满足品牌A的测试结果恰好有一次大于品牌B的测试结果的次数数出来,两个数据作比即可;(3)可以从题目中的条件中,从多个角度下结论,只要解释的有道理均可得分。
解析:
(Ⅰ)
|
|
|
|
|
|
|
|
|
|
|
|
1 | 2 | 4 | 6 | 2 | 4 | 4 | 2 | 1 | 6 | 4 | 7 |
所以![]() 等于1有2次,
等于1有2次, ![]() =2有3次,
=2有3次, ![]() =4有4次,
=4有4次, ![]() =6有2次,
=6有2次, ![]() =7有1次,
=7有1次,
则数据![]() 的众数为4
的众数为4
(Ⅱ)设事件D=“品牌![]() 的测试结果恰有一次大于品牌
的测试结果恰有一次大于品牌![]() 的测试结果”.
的测试结果”.
满足![]() 的测试共有4次,其中品牌
的测试共有4次,其中品牌![]() 的测试结果大于品牌
的测试结果大于品牌![]() 的测试结果有2次即测试3和测试7,不妨用M,N表示.品牌
的测试结果有2次即测试3和测试7,不妨用M,N表示.品牌![]() 的测试结果小于品牌
的测试结果小于品牌![]() 的测试结果有2次即测试6和测试11,不妨用P,Q表示.从中随机抽取两次,共有MN,MP,MQ,NP,NQ,PQ六种情况,其中事件D发生,指的是MP,MQ,NP,NQ四种情况.
的测试结果有2次即测试6和测试11,不妨用P,Q表示.从中随机抽取两次,共有MN,MP,MQ,NP,NQ,PQ六种情况,其中事件D发生,指的是MP,MQ,NP,NQ四种情况.
故![]() .
.
(Ⅲ)本题为开放问题,答案不唯一,在此给出评价标准,并给出可能出现的答案情况,阅卷时按照标准酌情给分.
给出明确结论,1分,结合已有数据,能够运用以下两个标准中的任何一个陈述得出该结论的理由,2分.
可能出现的作答情况举例,及对应评分标准如下:
结论一:,品牌![]() 处理器对含有文字与表格的文件的打开速度快一些,品牌
处理器对含有文字与表格的文件的打开速度快一些,品牌![]() 处理器对含有文字与图片的文件的打开速度快一些。
处理器对含有文字与图片的文件的打开速度快一些。
理由如下:从前6次测试(打开含有文字与表格的文件)来看,对于含有文字与表格的相同文件,品牌![]() 的测试有两次打开速度比品牌
的测试有两次打开速度比品牌![]() 快(数值小),品牌
快(数值小),品牌![]() 有四次比品牌
有四次比品牌![]() 快,从后6次测试(打开含有文字与图片的文件)来看,对于含有文字与图片的相同文件,品牌
快,从后6次测试(打开含有文字与图片的文件)来看,对于含有文字与图片的相同文件,品牌![]() 有四次打开速度比品牌
有四次打开速度比品牌![]() 快(数值小).
快(数值小).
结论二:从测试结果看,这两种国产品牌处理器的文件的打开速度结论:品牌![]() 打开文件速度快一些
打开文件速度快一些
理由如下:品牌![]() 处理器对文件打开的测试结果的平均数估计为
处理器对文件打开的测试结果的平均数估计为![]() ,品牌
,品牌![]() 处理器对文件打开的测试结果的平均数估计为
处理器对文件打开的测试结果的平均数估计为![]() ,所以品牌
,所以品牌![]() 打开文件速度快一些.(且品牌
打开文件速度快一些.(且品牌![]() 方差较小)
方差较小)


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的参数方程为
的参数方程为![]() ,其中
,其中![]() 为参数,且
为参数,且![]() 在直角坐标系
在直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求曲线![]() 的极坐标方程;
的极坐标方程;
(2)设![]() 是曲线
是曲线![]() 上的一点,直线
上的一点,直线![]() 被曲线
被曲线![]() 截得的弦长为
截得的弦长为![]() ,求
,求![]() 点的极坐标.
点的极坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上在第一象限内的点
上在第一象限内的点![]() 到焦点的距离为
到焦点的距离为![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 且垂直于
且垂直于![]() 轴.
轴.
(Ⅰ)求![]() 点的坐标;
点的坐标;
(Ⅱ)设不经过点![]() 和
和![]() 的动直线
的动直线![]() 交曲线
交曲线![]() 于点
于点![]() 和
和![]() ,交
,交![]() 于点
于点![]() ,若直线
,若直线![]() ,
,![]() ,
,![]() 的斜率依次成等差数列,试问:
的斜率依次成等差数列,试问:![]() 是否过定点?请说明理由.
是否过定点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 的右顶点,点
的右顶点,点![]() 是椭圆
是椭圆![]() 上不同的两点(均异于
上不同的两点(均异于![]() )且满足直线
)且满足直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .试判断直线
.试判断直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由.
是否过定点,若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为点
为点![]() 关于原点的对称点,点
关于原点的对称点,点![]() 在抛物线
在抛物线![]() 上,则下列说法错误的是( )
上,则下列说法错误的是( )
A. 使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有4个
有且仅有4个
B. 使得![]() 为直角三角形的点
为直角三角形的点![]() 有且仅有4个
有且仅有4个
C. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
D. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为点
为点![]() 关于原点的对称点,点
关于原点的对称点,点![]() 在抛物线
在抛物线![]() 上,则下列说法错误的是( )
上,则下列说法错误的是( )
A. 使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有4个
有且仅有4个
B. 使得![]() 为直角三角形的点
为直角三角形的点![]() 有且仅有4个
有且仅有4个
C. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
D. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018届高三·湖南十校联考)已知函数f(x)=x+sin x(x∈R),且f(y2-2y+3)+f(x2-4x+1)≤0,则当y≥1时, ![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. [1,3![]() -3] D.
-3] D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.曲线
轴正半轴为极轴,建立极坐标系.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为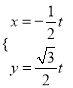 (
(![]() 为参数)
为参数)
(1)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的极坐标方程;
的极坐标方程;
(2)当![]() (
(![]() )时在曲线
)时在曲线![]() 上对应的点为
上对应的点为![]() ,若
,若![]() 的面积为
的面积为![]() ,求
,求![]() 点的极坐标,并判断
点的极坐标,并判断![]() 是否在曲线
是否在曲线![]() 上(其中点
上(其中点![]() 为半圆的圆心)
为半圆的圆心)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com