
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上在第一象限内的点
上在第一象限内的点![]() 到焦点的距离为
到焦点的距离为![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 且垂直于
且垂直于![]() 轴.
轴.
(Ⅰ)求![]() 点的坐标;
点的坐标;
(Ⅱ)设不经过点![]() 和
和![]() 的动直线
的动直线![]() 交曲线
交曲线![]() 于点
于点![]() 和
和![]() ,交
,交![]() 于点
于点![]() ,若直线
,若直线![]() ,
,![]() ,
,![]() 的斜率依次成等差数列,试问:
的斜率依次成等差数列,试问:![]() 是否过定点?请说明理由.
是否过定点?请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 恒过定点
恒过定点![]() .
.
【解析】试题分析:(1)抛物线![]() 上在第一象限内的点
上在第一象限内的点![]() 到焦点的距离为
到焦点的距离为![]() ,可求出n,得到抛物线方程,求导得斜率,写出切线方程;(2)设
,可求出n,得到抛物线方程,求导得斜率,写出切线方程;(2)设![]() ,联立抛物线方程,消元得
,联立抛物线方程,消元得![]() ,根据根与系数的关系
,根据根与系数的关系![]() ,
,![]() ,写出
,写出![]() ,
,![]() ,
,![]() 的斜率,根据成等差数列求不
的斜率,根据成等差数列求不![]() ,即可证明直线过定点.
,即可证明直线过定点.
试题解析:
(Ⅰ)由抛物线上的点![]() 到焦点的距离为
到焦点的距离为![]() ,得
,得![]() ,所以
,所以![]() ,则抛物线方程为
,则抛物线方程为![]() ,故曲线
,故曲线![]() 在点
在点![]() 处的切线斜率
处的切线斜率![]() ,切线方程为
,切线方程为![]() ,令
,令![]() 得
得![]() ,所以点
,所以点![]() .
.
(Ⅱ)由题意知![]() ,因为
,因为![]() 与
与![]() 相交,所以
相交,所以![]() .
.
设![]() ,令
,令![]() ,得
,得![]() ,故
,故![]() ,
,
设![]() ,
,![]() ,
,
由![]() 消去
消去![]() 得
得![]() ,则
,则![]() ,
,![]() ,直线
,直线![]() 的斜率为
的斜率为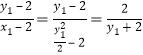 ,同理直线
,同理直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .因为直线
.因为直线![]() ,
,![]() ,
,![]() 的斜率依次成等差数列,
的斜率依次成等差数列,
所以![]() ,即
,即![]() ,即
,即![]() 整理得:
整理得:![]() ,
,
因为![]() 不经过点
不经过点![]() ,所以
,所以![]() ,所以
,所以![]() .故
.故![]() ,即
,即![]() 恒过定点
恒过定点![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() ,其焦距为2,离心率为
,其焦距为2,离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)设椭圆的右焦点为![]() ,
, ![]() 为
为![]() 轴上一点,满足
轴上一点,满足![]() ,过点
,过点![]() 作斜率不为0的直线
作斜率不为0的直线![]() 交椭圆于
交椭圆于![]() 两点,求
两点,求![]() 面积
面积![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究某药品的疗效,选取若干名志愿者进行临床试验,所有志愿者的舒张压数据(单位:kPa)的分组区间为[12,13),[13,14),[14,15),[15,16),[16,17],将其按从左到右的顺序分别编号为第一组,第二组,…,第五组,如图是根据试验数据制成的频率分布直方图.已知第一组与第二组共有20人,第三组中没有疗效的有6人,则第三组中有疗效的人数为( )

A. 6 B. 8
C. 12 D. 18
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点坐标为
的一个焦点坐标为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,过点
,过点![]() 的直线
的直线![]() (与
(与![]() 轴不重合)与椭圆
轴不重合)与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,试证明:直线
,试证明:直线![]() 与
与![]() 轴平行.
轴平行.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2018贵州遵义市高三上学期第二次联考】设抛物线![]() 的准线与
的准线与![]() 轴交于
轴交于![]() ,抛物线的焦点为
,抛物线的焦点为![]() ,以
,以![]() 为焦点,离心率
为焦点,离心率![]() 的椭圆与抛物线的一个交点为
的椭圆与抛物线的一个交点为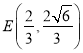 ;自
;自![]() 引直线交抛物线于
引直线交抛物线于![]() 两个不同的点,设
两个不同的点,设![]() .
.
(Ⅰ)求抛物线的方程和椭圆的方程;
(Ⅱ)若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】据中国日报网报道:2017年11月13日,TOP500发布的最新一期全球超级计算机500强榜单显示,中国超算在前五名中占据两席,其中超算全球第一“神威太湖之光”完全使用了国产品牌处理器。为了了解国产品牌处理器打开文件的速度,某调查公司对两种国产品牌处理器进行了12次测试,结果如下(数值越小,速度越快,单位是MIPS)
测试1 | 测试2 | 测试3 | 测试4 | 测试5 | 测试6 | 测试7 | 测试8 | 测试9 | 测试10 | 测试11 | 测试12 | |
品牌A | 3 | 6 | 9 | 10 | 4 | 1 | 12 | 17 | 4 | 6 | 6 | 14 |
品牌B | 2 | 8 | 5 | 4 | 2 | 5 | 8 | 15 | 5 | 12 | 10 | 21 |
设![]() 分别表示第次测试中品牌A和品牌B的测试结果,记
分别表示第次测试中品牌A和品牌B的测试结果,记![]()
![]()
(Ⅰ)求数据![]() 的众数;
的众数;
(Ⅱ)从满足![]() 的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
的测试中随机抽取两次,求品牌A的测试结果恰好有一次大于品牌B的测试结果的概率;
(Ⅲ)经过了解,前6次测试是打开含有文字和表格的文件,后6次测试是打开含有文字和图片的文件.请你依据表中数据,运用所学的统计知识,对这两种国产品牌处理器打开文件的速度进行评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() :
: ![]() 满足:
满足: ![]() ,
, ![]() 或1(
或1(![]() ).对任意
).对任意![]() ,都存在
,都存在![]() ,使得
,使得![]() .,其中
.,其中![]()
![]() 且两两不相等.
且两两不相等.
(I)若![]() .写出下列三个数列中所有符合题目条件的数列的序号;
.写出下列三个数列中所有符合题目条件的数列的序号;
①1,1,1,2,2,2;②1,1,1,1,2,2,2,2;③1,l,1,1,1,2,2,2,2
(Ⅱ)记![]() .若
.若![]() ,证明:
,证明: ![]() ;
;
(Ⅲ)若![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com