
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随机抽取![]() 人对共享产品对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
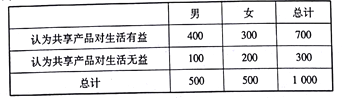
(Ⅰ)根据表中的数据,能否在犯错的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(Ⅱ)为了答谢参与问卷调查的人员,该公司对参与本次问卷调查的人员随机发放![]() 张超市的购物券,购物券金额以及发放的概率如下:
张超市的购物券,购物券金额以及发放的概率如下:
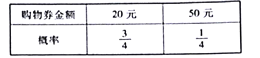
现有甲、乙两人领取了购物券,记两人领取的购物券的总金额为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:  .
.
临界值表:

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高三年级共有1000名学生,其中男生650人,女生350人,为了调查学生周末的休闲方式,用分层抽样的方法抽查了200名学生.
(Ⅰ)完成下面的![]() 列联表;
列联表;
不喜欢运动 | 喜欢运动 | 合计 | |
女生 | 50 | ||
男生 | |||
合计 | 100 | 200 |
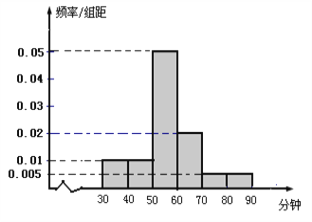
(Ⅱ)在抽取的样本中,调查喜欢运动女生的运动时间,发现她们的运动时间介于30分钟到90分钟之间,右图是测量结果的频率分布直方图,若从区间段![]() 和
和![]() 的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
的所有女生中随机抽取两名女生,求她们的运动时间在同一区间段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 上在第一象限内的点
上在第一象限内的点![]() 到焦点的距离为
到焦点的距离为![]() ,曲线
,曲线![]() 在点
在点![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 且垂直于
且垂直于![]() 轴.
轴.
(Ⅰ)求![]() 点的坐标;
点的坐标;
(Ⅱ)设不经过点![]() 和
和![]() 的动直线
的动直线![]() 交曲线
交曲线![]() 于点
于点![]() 和
和![]() ,交
,交![]() 于点
于点![]() ,若直线
,若直线![]() ,
,![]() ,
,![]() 的斜率依次成等差数列,试问:
的斜率依次成等差数列,试问:![]() 是否过定点?请说明理由.
是否过定点?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为![]() 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)将曲线![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角
的倾斜角![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,且椭圆的离心率为
上,且椭圆的离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若![]() 为椭圆
为椭圆![]() 的右顶点,点
的右顶点,点![]() 是椭圆
是椭圆![]() 上不同的两点(均异于
上不同的两点(均异于![]() )且满足直线
)且满足直线![]() 与
与![]() 斜率之积为
斜率之积为![]() .试判断直线
.试判断直线![]() 是否过定点,若是,求出定点坐标,若不是,说明理由.
是否过定点,若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 为点
为点![]() 关于原点的对称点,点
关于原点的对称点,点![]() 在抛物线
在抛物线![]() 上,则下列说法错误的是( )
上,则下列说法错误的是( )
A. 使得![]() 为等腰三角形的点
为等腰三角形的点![]() 有且仅有4个
有且仅有4个
B. 使得![]() 为直角三角形的点
为直角三角形的点![]() 有且仅有4个
有且仅有4个
C. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
D. 使得![]() 的点
的点![]() 有且仅有4个
有且仅有4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com