
已知x=1是函数f(x)=mx3-3(m+1)x2+nx+1的一个极值点,其中m、n∈R,m<0.
(1)求m与n的关系表达式;
(2)求f(x)的单调区间;
(3)当x∈[-1,1]时,函数y=f(x)的图象上任意一点的切线斜率恒大于3m,求m的取值范围.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
角α终边上的点P与A(a,2a)关于x轴对称(a>0),角β终边上的点Q与A关于直线y=x对称,求sin α·cos α+sin β·cos β+t an α·tan β的值.
an α·tan β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3+bx2-3x在x=±1处取得极值.
(1)讨论f(1)和f(-1)是函数f(x)的极大值还是极小值;
(2)过点A(0,16)作曲线y=f(x)的切线,求此切线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
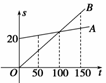
某电信公司推出两种手机收费方式:A种方式是月租20元,B种方
式是月租0元.一个月的本地网内打出电话时间t(分钟)与打出电话费s(元)的函数关系如图,当打出电话150分钟时,这两种方式电话费相差________元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com