
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点.
两个不同的点.
(1)试探究![]() 的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
的值是否为一个常数?若是,求出这个常数;若不是,请说明理由.
(2)记![]() 的面积为
的面积为![]() ,
, ![]() 的面积为
的面积为![]() ,令
,令![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】根据下列条件求双曲线的标准方程:
(1)经过点(![]() ,3),且一条渐近线方程为4x+3y=0.
,3),且一条渐近线方程为4x+3y=0.
(2)P(0,6)与两个焦点的连线互相垂直,与两个顶点连线的夹角为![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
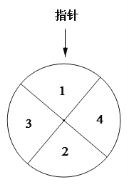
【题目】【2016高考山东文数】某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若![]() ,则奖励玩具一个;
,则奖励玩具一个;
②若![]() ,则奖励水杯一个; ③其余情况奖励饮料一瓶.
,则奖励水杯一个; ③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】路灯距地面8 m,一个身高为1.6 m的人以84 m/min的速度在地面上从路灯在地面上射影点C沿某直线离开路灯.
(1)求身影的长度y与人距路灯的距离x之间的关系式;
(2)求人离开路灯的第一个10 s内身影的平均变化率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com