
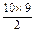 d=15×20+
d=15×20+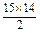 d,
d, . 4分
. 4分 )=-
)=- n+
n+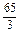 . 8分
. 8分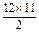
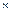 (-
(- )="130. " 14分
)="130. " 14分 . 4分
. 4分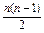 ·(-
·(- )
)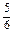 n2+
n2+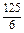 n
n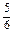
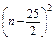 +
+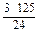 . 8分
. 8分 . 4分
. 4分

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:高中数学 来源:不详 题型:解答题
 ,an=2-
,an=2-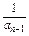 (n≥2,n∈N*),数列{bn}满足bn=
(n≥2,n∈N*),数列{bn}满足bn= (n∈N*).
(n∈N*).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
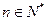 ,不等式
,不等式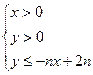 所表示的平面区域为
所表示的平面区域为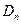 ,把
,把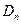 内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列:
内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列: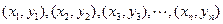
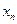 ,
,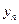 ;
;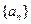 满足
满足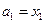 ,且
,且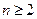 时
时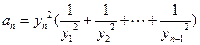 .证明当
.证明当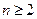 时,
时,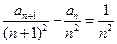 ;
;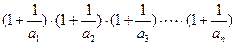 与4的大小关系.
与4的大小关系.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
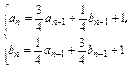 (n≥2).
(n≥2).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
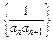 的前n项和Tn.
的前n项和Tn.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 |  | ||||||||||||||
|
| ||||||||||||||
 |  | ||||||||||||||
| |||||||||||||||
| |||||||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com