
分析 (1)由A与B,求出两集合的交集与并集即可;
(2)由全集U,求出A补集与B补集的交集,求出A,B以及C的交集即可.
解答 解:(1)∵A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},
∴A∪B={1,2,4,5,6,7,8,9,10},A∩B={4};
(2)∵全集U={x∈N|x≤10}={0,1,2,3,4,5,6,7,8,9},
集合A={1,2,4,5,9},B={4,6,7,8,10},C={3,5,7},
∴∁UA={0,3,6,7,8},∁UB={0,1,2,3,5,9},
则(∁UA)∩(∁UB)={0,3},A∩B∩C=∅.
点评 此题考查了交、并、补集的混合运算,熟练掌握各自的定义是解本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | S10≤S9 | B. | S10<S11 | C. | S10=S9 | D. | S10=S11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<b<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
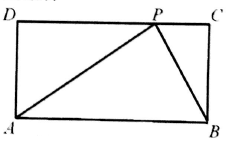
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{2}-1$ | D. | $\sqrt{3}-1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com