
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{6}$ | C�� | $\frac{1}{4}$ | D�� | $\frac{1}{2}$ |
���� �ӳ�OC��D��ʹOD=4OC���ӳ�CO��AB��E������֪��OΪ��DABC���ģ�EΪAB�е㣬�Ƶ���S��AEC=S��BEC��S��BOE=2S��BOC���ɴ�����������
��� 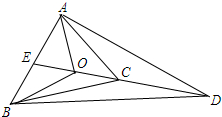 �⣺�ӳ�OC��D��ʹOD=4OC��
�⣺�ӳ�OC��D��ʹOD=4OC��
�ӳ�CO��AB��E��
��OΪ��ABC��һ�㣬������$\overrightarrow{OA}+\overrightarrow{OB}+4\overrightarrow{OC}=\overrightarrow{0}$��
��$\overrightarrow{OD}+\overrightarrow{OA}+\overrightarrow{OB}$=$\overrightarrow{0}$��
��OΪ��DABC���ģ�EΪAB�е㣬
��OD��OE=2��1����OC��OE=1��2����CE��OE=3��2��
��S��AEC=S��BEC��S��BOE=2S��BOC��
�ߡ�OBC���ABC������ֱ�ΪS1��S2��
��$\frac{{S}_{1}}{{S}_{2}}$=$\frac{1}{6}$��
��ѡ��B��
���� ���⿼�����������������ֵ�������е��⣬����ʱҪ�������⣬ע�����������������ĵ�֪ʶ�ĺ������ã�


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+y2��5 | B�� | $\frac{y}{x-2}$��-2 | C�� | 2x+y��5 | D�� | |x+3y-1|��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�-2���ȣ�2��+�ޣ� | B�� | ��-�ޣ�-2���ȣ�1��2�� | C�� | ��-2��1���ȣ�2��+�ޣ� | D�� | ��-2��1���ȣ�1��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com