
| A. | 向左平移$\frac{π}{3}$个单位长度 | B. | 向右平移$\frac{π}{3}$个单位长度 | ||
| C. | 向左平移$\frac{π}{6}$个单位长度 | D. | 向右平移$\frac{π}{6}$个单位长度 |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2006 | 2008 | 2010 | 2012 | 2014 |
| 年需求量(万吨) | 257 | 276 | 286 | 298 | 318 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“?x∈R,x2-x+1≥$\frac{3}{4}$”的否定是“?x0∈R,x02-x0+1<$\frac{3}{4}$” | |
| B. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| C. | 命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | |
| D. | 若命题“非p”与命题“p或q”都是真命题,那么q一定是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
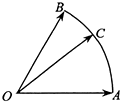 己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )
己知C是半径为1、圆心角为60°的圆弧上的动点,如图,若$\overrightarrow{OC}$=x$\overline{OA}$+y$\overrightarrow{OB}$,其中x,y∈R,则x+y的最大值是( )| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\frac{4}{3}$ | C. | 2 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
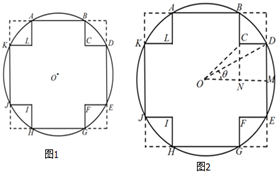 如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)
如图在半径为5cm的圆形的材料中,要截出一个“十字形”ABCDEFGHIJKL,其为一正方形的四角截掉全等的小正方形所形成的图形.(O为圆心)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com