
分析 (1)根据a=$\frac{7}{2}$,求出集合N,根据集合的基本运算即可求M∪N,(∁UM)∩N;
(2)根据M?N,建立条件关系即可求实数a的取值范围.
解答 解:(1)由题意:M={x|-2≤x≤5},
则∁RM={x|x>5或x<-2},
当a=$\frac{7}{2}$时,N={x|a+1≤x≤2a-1}={x|$\frac{9}{2}≤x≤6$}.
∴M∪N={x|-2≤x≤6},
(∁RM)∩N={x|5<x≤6}.
(2)∵M?N,
∴当N=∅时,满足题意,此时,2a-1<a+1,解得:a<2;
当N≠∅时,要使M?N成立,则需满足$\left\{\begin{array}{l}{a+1≤2a-1}\\{a+1≥-2}\\{2a-1≤5}\end{array}\right.$,
解得:2≤a≤3.
综上所得,实数a的取值范围是(-∞,3].
点评 本题主要考查集合的基本运算,比较基础.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 1000×(1+5×5%)万元 | B. | 1000×(1+5%)5万元 | ||
| C. | $1000×\frac{{1.05×(1-{{1.05}^4})}}{1-1.05}万元$ | D. | $1000×\frac{{1.05×(1-{{1.05}^2})}}{1-1.05}万元$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向右平移个单位$\frac{π}{3}$ | B. | 向右平移个单位$\frac{π}{6}$ | ||
| C. | 向左平移个单位$\frac{π}{3}$ | D. | 向左平移个单位$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
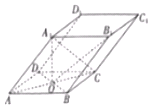 如图,四棱柱ABCD-A1B1C1D1的底面AB是CD菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.
如图,四棱柱ABCD-A1B1C1D1的底面AB是CD菱形,AC∩BD=O,A1O⊥底面ABCD,AB=AA1=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,D是Rt△BAC斜边BC上的一点,AC=$\sqrt{3}$DC.
如图,D是Rt△BAC斜边BC上的一点,AC=$\sqrt{3}$DC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com