
| A. | f(x)=-x3 | B. | f(x)=$\sqrt{-x}$ | C. | f(x)=-tanx | D. | f(x)=$\frac{1}{x}$ |
分析 根据函数的奇偶性的定义,单调性的定义判断:①f(x)=-x3是奇函数又是减函数;②f(x)=$\sqrt{-x}$,定义域(-∞,0]不是奇函数;
③f(x)=-tanx在定义域上不是减函数;④f(x)=$\frac{1}{x}$在定义域上不是减函数;即可判断f(x)=-x3是奇函数又是减函数,从而可得答案.
解答 解:①∵f(x)=-x3,定义域为(-∞,+∞),
∴f(-x)=-f(x),x1<x2,则-x13$>-{x}_{2}^{3}$,
∴f(x)=-x3是奇函数又是减函数,
②∵f(x)=$\sqrt{-x}$,定义域(-∞,0]
∴f(x)=$\sqrt{-x}$不是奇函数,
③f(x)=-tanx在定义域上不是减函数,
④f(x)=$\frac{1}{x}$在定义域上不是减函数,
故选;A
点评 本题考查了常见函数的单调性,奇偶性,注意定义域,单调区间的定义,属于中档题.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
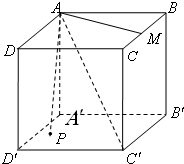 如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )
如图,正方体ABCD-A′B′C′D′中,M为BC边的中点,点P在底面A′B′C′D′上运动并且使∠MAC′=∠PAC′,那么点P的轨迹是( )| A. | 一段圆弧 | B. | 一段椭圆弧 | C. | 一段双曲线弧 | D. | 一段抛物线弧 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{π}{3}$个单位而得到 | B. | 向右平移$\frac{π}{3}$个单位而得到 | ||
| C. | 向左平移$\frac{π}{6}$个单位而得到 | D. | 向右平移$\frac{π}{6}$个单位而得到 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com