
分析 求出集合P,及满足从P中随机的取一元素x,恰使lgx有意义的区间,代入几何概型概率计算公式,可得答案
解答 解:∵关于x的方程x2+mx-$\frac{1}{2}$m+$\frac{15}{4}$=0至多有一个实根(相等的根只能算一个),
∴m2-4(-$\frac{1}{2}$m+$\frac{15}{4}$)≤0,
解得-5≤m≤3,
故P=[-5,3],
使得式子lgm有意义,则0<m≤3,
故任取一个元素m,求使得式子lgm有意义的概率为$\frac{3-0}{3-(-5)}$=$\frac{3}{8}$
点评 本题考查的知识点是几何概型概率计算公式,计算出满足条件和所有基本事件对应的几何量,是解答的关键,难度中档.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | 1 | C. | 2($\sqrt{2}$-1) | D. | $\sqrt{2}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2(1-m)}}{2}$ | B. | $\frac{\sqrt{2(1+m)}}{2}$ | C. | $±\frac{\sqrt{2(1-m)}}{2}$ | D. | $±\frac{\sqrt{2(1+m)}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}{a^2}$ | B. | $\frac{{\sqrt{3}}}{3}{a^2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
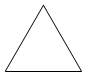 一个正三棱柱的侧棱长和底面边长相等,体积为$16\sqrt{3}c{m^3}$,它的三视图中的俯视图如图所示,侧视图是一个矩形,则侧视图的面积是( )
一个正三棱柱的侧棱长和底面边长相等,体积为$16\sqrt{3}c{m^3}$,它的三视图中的俯视图如图所示,侧视图是一个矩形,则侧视图的面积是( )| A. | 8 | B. | $8\sqrt{3}$ | C. | 4 | D. | $4\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com