Question

7．设E，F分别是边长为1的正方形ABCD的边BC，CD上的点，∠EAF=45°，则$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值等于（　　）

• A． $\sqrt{2}$
• B． 1
• C． 2（$\sqrt{2}$-1）
• D． $\sqrt{2}$-1

Answer 1

分析 以A为坐标原点，AB，AD所在的直线为x，y轴建立直角坐标系，设E（1，m），F（n，1），求得tan∠EAB=m，tan∠FAD=n，由两角和的正切公式可得tan（∠EAB+∠FAD）=1，即有m+n+mn=1，运用基本不等式可得mn≤（$\frac{n+m}{2}$）²，解m+n的不等式即可得到所求最小值．

解答 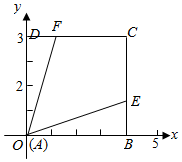解：以A为坐标原点，AB，AD所在的直线为x，y轴建立直角坐标系，
设E（1，m），F（n，1），
tan∠EAB=m，tan∠FAD=n，
且tan（∠EAB+∠FAD）=tan（90°-∠EAF）=tan45°=1，
即有$\frac{tan∠EAB+tan∠FAD}{1-tan∠EAB•tan∠FAD}$=$\frac{m+n}{1-mn}$=1，
即为m+n+mn=1，
则$\overrightarrow{AE}$•$\overrightarrow{AF}$=（1，m）•（n，1）=m+n，
由mn≤（$\frac{n+m}{2}$）²，可得1=m+n+mn≤（m+n）+$\frac{（m+n）^{2}}{4}$，
解不等式可得m+n≥2（$\sqrt{2}$-1），
当且仅当m=n时，$\overrightarrow{AE}$•$\overrightarrow{AF}$的最小值为2（$\sqrt{2}$-1），
故选：C．

点评 本题考查向量的数量积的坐标表示和最值的求法，注意运用基本不等式和两角和的正切公式，考查化简整理的运算能力，属于中档题．