
己知四棱锥P-ABCD,其中底面ABCD为矩形,侧棱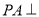 底面ABCD,其中BC=2AB=2PA=6,
底面ABCD,其中BC=2AB=2PA=6,
M,N为侧棱PC上的两个三等分点,如图所示:

(1)求证: AN∥平面MBD;
(2)求锐二面角B-PC-A的余弦值.
(1)证明见解析;(2)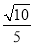 .
.
【解析】
试题分析:(1)构造三角形,利用三角形的中位线证明线线平行,再利用线面平行的判定定理进行证明;
(2)联立空间直角坐标系,利用空间向量进行求解.
解题思路:证明线面平行的一般思路:
①利用线面平行的判定定理进行证明,即:利用平行四边形、梯形、三角形的中位线构造线线平行;
②利用面面平行的性质,即构造面面平行.
试题解析:(1)证明:连结AC交BD于O,连结OM,
∵底面ABCD为矩形,∴O为AC中点,∵M、N为侧棱PC的三等份点,∴CM=CN,
∴OM//AN, ∵OM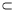 平面MBD,AN
平面MBD,AN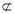 平面MBD,∴AN//平面MBD
平面MBD,∴AN//平面MBD
(2)易知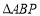 为等腰直角三角形,所以BP为外接圆的直径,所以PB=
为等腰直角三角形,所以BP为外接圆的直径,所以PB=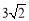 ,PA=3
,PA=3
如图所示,以A为原点,建立空间直角坐标系A-xyz,
则A(0,0,0),B(3,0,0),C(3,6,0),D(0,6,0),P(0,0,3),M(2,4,1),N(1,2,2),
设平面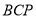 的法向量为
的法向量为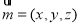 ,
,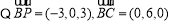 ,并且
,并且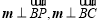 ,
,
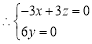 ,令
,令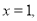 得
得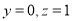 ,
,
∴平面MBD的一个法向量为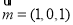 ,
,
设平面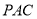 法向量为
法向量为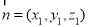 ,
,
同理可得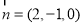
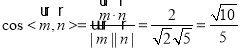
由图可知,二面角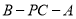 为锐角,
为锐角,
∴二面角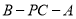 的余弦值为
的余弦值为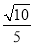
考点:1.线面平行的判定定理;2.二面角.
考点分析: 考点1:点、线、面之间的位置关系 考点2:异面直线所成的角 考点3:线面所成的角 试题属性

科目:高中数学 来源:2014-2015学年江西省高一上学期期末考试数学试卷(解析版) 题型:选择题
已知四边形ABCD的三个顶点A(0,2),B(-1,-2),C(3,1),且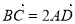 ,则D的坐标为
,则D的坐标为
A.(2,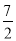 ) B.(2,-
) B.(2,- ) C.(3,2) D.(1,3)
) C.(3,2) D.(1,3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年吉林省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
已知AB是抛物线 的一条过焦点的弦,且|AB|=4,则AB中点C的横坐标是( )
的一条过焦点的弦,且|AB|=4,则AB中点C的横坐标是( )
A.2 B. C.
C. D.
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com