
分析 由于圆C的方程为(x-3)2+y2=1,由题意可知,只需(x-3)2+y2=4与直线y=2kx-2有公共点即可.
解答 解:∵圆C的方程为x2+y2-6x+8=0,整理得:(x-3)2+y2=1,即圆C是以(3,0)为圆心,1为半径的圆;
又直线y=2kx-2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴只需圆C′:(x-3)2+y2=4与直线y=2kx-2有公共点即可.
设圆心C′(3,0)到直线y=2kx-2的距离为d,
则d=$\frac{|6k-2|}{\sqrt{4{k}^{2}+1}}$≤2,即5k2-6k≤0,
∴k∈$[0,\frac{6}{5}]$,
故答案为$[0,\frac{6}{5}]$.
点评 本题考查直线与圆的位置关系,将条件转化为“(x-3)2+y2=4与直线y=2kx-2有公共点”是关键,考查学生灵活解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
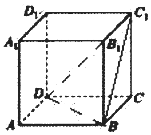 在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )
在正方体ABCD-A1B1C1D1中,过点A作平面α平行平面BDC1,平面α与平面A1ADD1交于直线m,平面α与平面A1ABB1交于直线n,则直线m与直线n所成的角为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
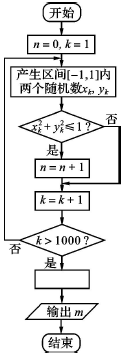
| A. | $m=\frac{n}{4000}$ | B. | $m=\frac{n}{1000}$ | C. | $m=\frac{n}{500}$ | D. | $m=\frac{n}{250}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 294 | B. | 174 | C. | 470 | D. | 304 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com